Considere o campo vetorial em definido por
(a) Calcule o divergente do campo
(b) Calcule diretamente o fluxo de através da esfera , em relação ao campo normal que aponta para fora da esfera
(c) Explique porque não é correto usar o Teorema da Divergência para efetuar o cálculo acima.
(d) Calcule o fluxo de através do elipsoide , em relação ao campo normal que aponta para fora do elipsoide.
Sugestão: Aplique o Teorema da Divergência na região do espaço limitada pelas superfícies do elipsoide e da esfera
Passo 1
Letra (a)
O divergente de um campo pode ser dado por
Vamos derivar esse campo aí com calma
As contas são muito parecidas pras outras derivadas
O divergente é a soma disso tudo
Passo 2
Letra (b)
Para calcular diretamente o fluxo através da esfera precisamos calcular a integral de superfície, certo? Essa aqui
Precisamos então parametrizar a superfície, calcular a normal e integrar tudo. Vamos fazer passo a passo aqui
Começando pela superfície, temos uma esfera de raio
Só dois parâmetros mesmo, é uma superfície lembra? Não um sólido!
Os limites são
Passo 3
Vamos agora para o vetor normal dessa superfície
Mas queremos a normal apontando para fora, portanto o sinal é o oposto
Passo 4
Temos a normal, temos a parametrização. Antes de jogar na integral, vamos substituir os novos parâmetros em
Com a parametrização
Temos que
Portanto
Agora sim, com tudo isso na integral
Integrando isso aí
Passo 5
Letra (c)
O teorema da divergência (teorema de Gauss) nos diz que
Seria perfeito pra gente né? O divergente de é igual a zero, a integral tripla seria zero!
O problema são as considerações que fazemos para usar esse teorema, lembra de todas elas?
(i) O vetor normal deve estar apontando para fora do sólido
(ii) A superfície é a fronteira de , ou seja
(iii) Não podemos ter singularidades no campo na região definida por
O problema de usar o teorema aqui é que não respeitamos essa terceira hipótese. O campo não existe no ponto , já que o denominador fica zero.
Como a esfera possui a origem, não podemos usar o teorema aqui.
Passo 6
Letra (d)
Vamos entender primeiro como é esse elipsoide
Fazer a integral direta desse cara vai ser bem impossível, o denominador do campo não vai ser igual a que nem aconteceu na letra (b).
Vamos tentar usar o teorema de Gauss aqui como disse a sugestão
“Ué, mas não acabamos de provar que não pode usar o teorema por causa do ponto ?”
Dá pra usar o teorema se o nosso sólido não tiver esse ponto, aí tudo bem! Olha só o esboço
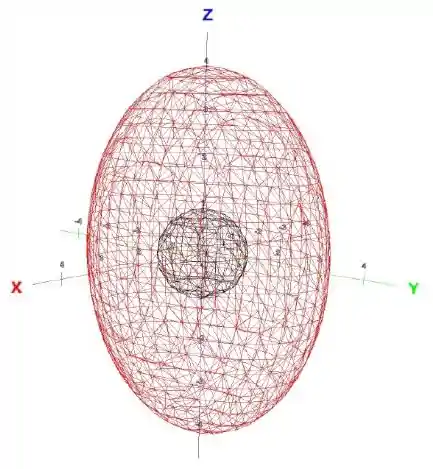
Viu que não estamos incluindo a origem no sólido? Estamos pegando a região entre a esfera () e o elipsoide ()
Tome cuidado com a orientação das superfícies só! Calculamos a integral da esfera com a normal apontada para fora, essa esfera aqui tem que ter a normal apontada pra dentro.
Ve se ajuda isso aqui
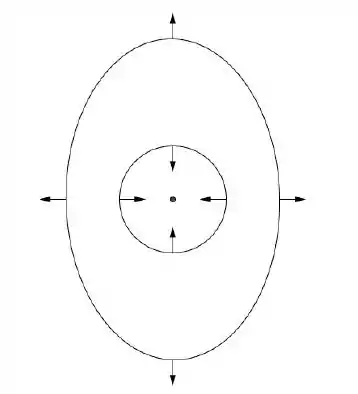
O teorema de Gauss fica assim
Passo 7
Bom, já calculamos o divergente que é zero, portanto
Também já calculamos a integral de superfície de
É só colocar tudo no teorema então
Resposta
(a)
(b)
(d)