Seja
Calcule , onde é a parte do parabolóide com , orientada com a normal unitária .
Passo 1
Ele quer aquela integral de superfície ao longo daquela função , repara que ele colocou essa parada divida em duas funções, vamos pensar então na como
Com
E
Vamos fazer cada uma das integrais para cada um desses dois campos separado e depois é só somar.
Passo 2
Vamos começar fazendo
Para isso, precisamos parametrizar , certo? Como se trata de um paraboloide, e paraboloide ficam “bem” em coordenadas cilíndricas, são elas que vamos usar:
Levando para a equação do paraboloide, temos:
Ou seja, sua parametrização é:
Onde
O que quer dizer que .
Como se trata de uma volta completa em torno de , .
Passo 3
Agora vamos calcular a normal à superfície:
Passo 4
Agora vamos montar a integral. Escrevendo o campo em função da parametrização:
Levando tudo o que temos para a integral:
Lembrando que
Passo 5
Agora a gente precisa calcular a outra parte da integral
Mas esse campo tem uma expressão bizarra, não é?
Vamos calcular o divergente disso aí então e rezar pra ser algo bonito:
Olha que maravilha!!
Passo 6
Partiu usar Gauss então, né? MUITA CALMA NESSA HORA. A gente precisa de uma superfície fechada para aplicar o teorema.
Nossa superfície é essa aqui:
Nada mais natural que fechar isso aí com um círculo embaixo, né? Agora olha de novo para o campo:
Repara que ele não está definido em , ou seja: NÃO PODEMOS fechar com esse círculo nem com qualquer superfície que contenha a origem.
Precisamos tirar a origem da região. Ok, como temos vários termos quadráticos no campo, vamos fazer isso com uma casa de esfera:
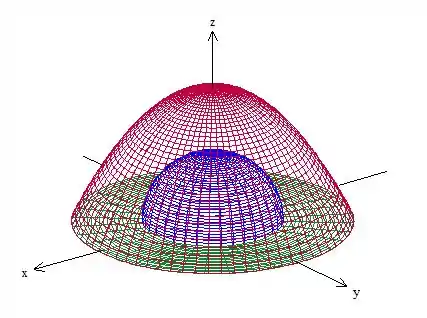
Pronto, isolamos a origem. Assim, a fronteira da região passa a de o paraboloide , com a semiesfera e o anel plano .
Que bagunça, né? É a vida, vamos lá. Finalmente, podemos apicar Gauss:
Foi? Então, a integral que queremos é isso aqui:
Onde as normais apontam para fora de .
Passo 7
Calma, gente, tá acabando. Precisamos, então, dessas duas integrais. Vamos começar pelo anel que pertence ao plano .
Tá, como nós sabemos que o raio máximo do paraboloide é (pelo enunciado), vamos assumir que essa nossa esfera tem raio . Agora precisamos parametrizar o anel, certo?
Repara que a sua parametrização vai ser uma coisa assim:
Onde .
E sua normal vai ser uma coisa assim:
Beleza? Agora olha isso aqui:
Escrevendo o campo em função da parametrização, temos:
Agora chora de alegria comigo:
Por milagre divino esse produto escalar é zero :D É, só que a questão ainda não acabou.
Passo 8
Agora vamos calcular a integral na esfera .
Lembrando que
Respira fundo e vamos continuar, essa questão é levemente gigante né mas fazer o que.
Para achar o vetor normal vamos fazer
Então
Fica atento a orientação do vetor, que deve estar orientado para fora de , portanto, para baixo na esfera. Então, como, vetor normal na verdade vai ser trocando o sinal desse vetor que achamos
Um detalhe importante é que quando achamos o vetor normal pelo gradiente temos que normalizar esse vetor, vamos fazer
Lembrando que para essa esfera temos
A nossa integral vai ficar
Lembra também que em vamos ter
Então
Então queremos a área da metade de uma esfera de raio , então
Assim nossa integral de superfície vai ficar
Passo 9
Vamos juntar a parada toda agora
E nós temos:
Portanto, o que queremos é:
ALELUIA!!!