Calcule
onde
e é parte da superfície com , orientada de modo que é tal que .
Passo 1
Ele quer aquela integral de superfície ao longo daquela função , repara que ele colocou essa parada divida em duas funções, vamos pensar então na como
Com
E
Vamos fazer cada uma das integrais para cada um desses dois campos separado e depois é só somar.
Passo 2
Vamos começar fazendo
Aqui temos que parametrizar a superfície , mas olha a sua fórmula de novo
Consegue perceber que depende tanto de quando de ? Então vamos fazer
Ele disse que , então
Passo 3
Agora vamos achar o vetor normal a essa superfície
Primeiro temos que achar as derivadas em relação a e em relação a
E
O nosso vetor vai ficar
Vamos conferir aquela parada que ele pediu, ou seja,
Ok deu maior que , então o vetor normal é esse mesmo, caso esse produto escalar desse negativo era só trocar o sentido do vetor .
Passo 4
A nossa integral vai ficar
Isso na verdade é a integral dupla ao longo da região
Vamos ver como trabalhar com essa região aí no próximo passo
Passo 5
Essa região é
Repara que isso é a parte de dentro da elipse
Então vamos usar coordenadas cilíndricas dando aquela adaptada para a elipse, colocando os coeficientes da elipse na fórmula para “transformar” numa circunferência de raio , fazendo
Aqui vamos ter e
Não pode esquecer do jacobiano, ele vai ser o jacobiano das coordenadas polares, multiplicando por e por , então
Passo 6
A nossa integral dupla vai ficar
Aqui podemos fazer
A nossa integral vai ficar
Isso nos diz que
Essa integral no Gabarito está com o valor diferente, mas se você repara eles fizeram a superfície errada, para o cálculo em ele fazem
Quando na verdade seria no lugar de ali.
Passo 7
Vamos agora achar a integral de superfície de , ou seja
Aqui se tentarmos fazer a parada pela definição a conta vai ficar mostrar, sabe porque? Se fizéssemos aquela parametrização de teríamos que substituir isso em
Tá vendo um maldito ali? Isso vai fazer nossa conta ficar surreal de gigante. Então precisamos fazer outra parada. A ideia é usar o teorema de Gauss para tentar melhorar a cara dessa integral que temos que fazer. MAAAAAS temos dois problemas ao tentar usar Gauss, consegue ver? Primeiro temos que a função não é definida na origem, se a superfície incluir a origem não podemos usar Gauss.
Vamos ver como é a superfície
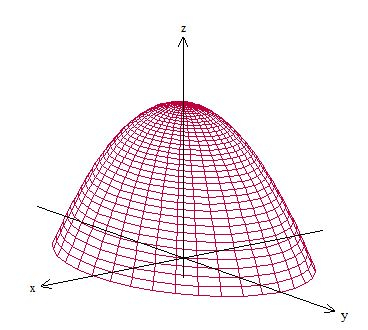
Isso nos mostra que ela inclui a origem, o outro problema é que essa superfície não é fechada.
Temos que fechar essa superfície , o mais interessante seria colocar a tampa na parte de baixo, ou seja, fazer
Com
Mas isso ainda inclui a origem na nossa conta, vamos fazer um buraco na origem, colocando uma semi esfera de raio , assim teríamos algo assim tampando tudo
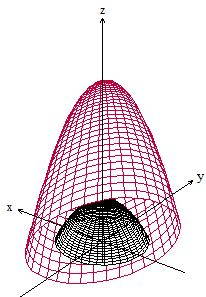
Tá vendo a esfera ali dentro? Isso vai mudar a nossa tampa, ela vai ser a parte de dentro de
E a parte de fora de
Sacou? São as duas bases.
Vamos ter
Onde
E
Essa é a tampa dentro do paraboloide e fora da esfera.
E
Essa é a esfera preta.
Uma parada que temos que tomar cuidado é como vão ser os vetores normais, repara que ele deu a orientação para quando ele diz que significa que a parada vai apontar para fora, isso porque ele está dizendo que a componente vai ser positivo.
Quando aplicamos Gauss a orientação dos vetores normais vai ser para fora de , ou seja, em é para cima, e em e é para baixo.
Passo 8
Ufa, depois de contornar muito problemas dessa parada podemos aplicar Gauss em sem problema. Vamos ter
Vamos escrever aquela integral de superfície separa em , e
Vamos começar achando o divergente de
Beleza, isso nos faz ter uma conta a menos rs, que seria aquela integral tripla. Vamos ter
Passo 9
Vamos começar fazendo a integral dupla de
Lembrando que
Isso é a parte do plano limitada pela esfera e o paraboloide. Vamos fazer
E o vetor normal vai ser
Fica atento a orientação do vetor, eu falei ali em cima que para deve ser para baixo, então o vetor normal na verdade vai ser trocando o sinal desse vetor que achamos
A nossa integral vai ficar
Repara que em vamos ter , então podemos fazer essa substituição na integral, e a integral vai ficar
Beleza, temos uma integral já
Passo 10
Vamos agora para a outra integral de linha
Lembrando que
Respira fundo e vamos continuar, essa questão é levemente gigante né mas fazer o que.
Para achar o vetor normal vamos fazer
Então
Fica atento a orientação do vetor, eu falei ali em cima que para deve ser para baixo, então como vetor normal na verdade vai ser trocando o sinal desse vetor que achamos
Um detalhe importante é que quando achamos o vetor normal pelo gradiente temos que normalizar esse vetor, vamos fazer
Lembrando que para essa esfera temos
A nossa integral vai ficar
Lembra também que em vamos ter
Então
Então queremos a área da metade de uma esfera de raio , então
Assim nossa integral de superfície vai ficar
Passo 11
Vamos juntar a parada toda agora
Passo 12
Ufa, achamos a integral de superfície em e em , agora é só somar