Seja
Calcular onde S é a esfera , orientada com a normal saindo.
Passo 1
Como queremos a integral de superfície de uma esfera podemos utilizar o teorema de Gauss:
Temos que primeiro verificar se todas as condições são satisfeitas:
- A superfície deve ser fechada e assim definir um volume
- Não deve possuir singularidade
- A normal deve ser orientada para fora, no sentido contrário ao espaço definido pela superfície.
A única condição que não é satisfeita é a de singularidade, pois o ponto não está definido no nosso campo vetorial, por isso devemos eliminá-la hehehe
Passo 2
Para eliminar a singularidade, podemos utilizar uma esfera de raio um e centrada na origem para facilitar as nossas contas e que deve estar orientada com a normal apontando para o centro. Dessa forma a esfera e a superfície que o problema deu irão delimitar um volume entre essas duas superfícies.
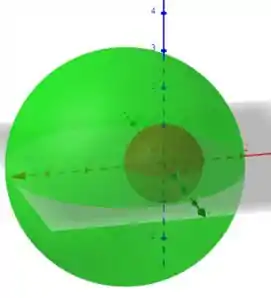
Obs.: Atenção para a orientação da normal à superfície. Para a esfera mais externa a orientação deve ser se afastando da origem e da esfera mais interna, a orientação deve ser para a origem. É só lembrar que a orientação deve estar contrária ao volume delimitado pelas duas superfícies.
Passo 3
Temos então que pelo Teorema de Gauss:
Onde W é o espaço confinado entre a esfera do problema e a esfera
Calculando o divergente do campo vetorial :
Onde:
Realizando a conta do divergente podemos ver que o resultado é 3. Assim:
Essa integral tripla da direita é nada mais nada menos que 3 vezes o volume do espaço .
Esse volume pode ser calculado como o volume da esfera verde menos o volume da esfera vermelha.
Para a verde: Volume =
Para a vermelha: Volume =
Então a nossa integral será:
Passo 4
Falta agora calcularmos a integral dupla que apareceu quando tivemos que adicionar a esfera de raio um para eliminarmos a singularidade.
Passo 5
Primeiro devemos parametrizar nossa superfície:
Onde R = 1
Nossa integral será calculada por:
Calculando
Para a segunda parte da integral:
Ficamos então com
O resultado dessa integral será então
Para finalizar iremos só substituir os valores das integrais que temos e assim: