Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Singularidade

Ver Teoria
Exercício 14123456789101112131516

Enunciado

Questão 5) Sejam r → = x i → + y j → + z k → , r = r → (magnitude do vetor) e S uma superfície fechada qualquer contendo a origem. Calcule

∬ S   r → r 3 ⋅ d S →

Passo 1

Antes de qualquer coisa vamos entender quem é essa função vetorial:

r → = x i → + y j → + z k →       →           r = x 2 + y 2 + z 2

Então a função F → x ,   y ,   z que vamos calcular a integral de superfície dela é...

F → x ,   y ,   z = r → r 3 = x x 2 + y 2 + z 2 3 2 ,   y x 2 + y 2 + z 2 3 2 ,   z x 2 + y 2 + z 2 3 2    

Sacou?

Passo 2

Então queremos a integral de superfície dessa função vetorial em cima de S que é uma superfície fechada qualquer que contenha a origem:

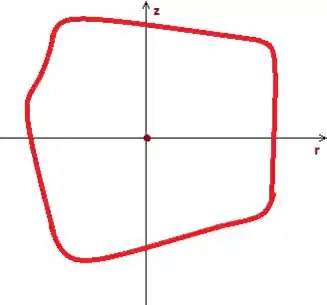
(Representa uma superfície fechada, só que seccionada pra você ver melhor ;)

Perceba que como não temos informação nenhuma sobre essa superfície (apenas que ela é uma qualquer) com certeza não vamos fazer essa questão pelo modo direto, pois precisaríamos dela. Por isso a ideia aqui é pensar em Gauss:

∬ S   F → ⋅ d S → = ∭ W   d i v   F → d V

Agora, essa integral não pode ser aplicada assim... De qualquer maneira. Precisamos garantir as condições do Teorema que nos pede:

1º - Uma superfície fechada S contendo o sólido W no seu interior.

2º - Um campo F → sem singularidades onde estamos trabalhando.

3º - Vetores normais saindo do sólido.

Passo 3

A primeira exigência está sendo satisfeita, pois a superfície é fechada (maluca, mas fechada) e delimita um sólido no seu interior.

Já a segunda... Do campo não ter singularidades essa falha, pois veja:

F → x ,   y ,   z = x x 2 + y 2 + z 2 3 2 ,   y x 2 + y 2 + z 2 3 2 ,   z x 2 + y 2 + z 2 3 2  

Se você substituir o ponto 0 ,   0 ,   0 , vai dar ruim a fração! Por isso o que Gauss faz? Vai lá e tira esse ponto problemático fora do sólido. Com o que? Com outra superfície:

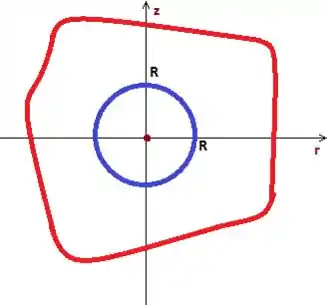
Em tese pode ser qualquer superfície, mas é melhor pegar uma esfera nesse caso, saca? Uma esfera que esteja dentro do sólido. Como não o conhecemos o sólido, vamos supor que uma esfera de raio R conhecido cabe inteiramente dentro de W :

x 2 + y 2 + z 2 = R 2

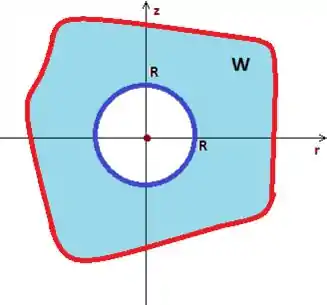
Passo 4

Show, só está faltando à condição de orientado positivamente, o que pra nossa alegria o problema não fala pra que direção ele quer o vetor normal na superfície bizarra W , por isso vamos supor que sim, ele está saindo do sólido:

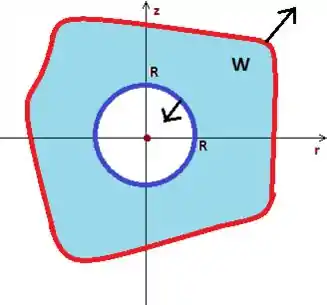
Passo 5

Aplicando o Teorema...

∬ ∂ W   F → ⋅ d S → = ∭ W   d i v   F → d V

Mas veja aqui você que o teorema nos dá a igualdade, mas é válida só para integrais de superfície sobre a borda ∂ W . Como a borda aqui é composta por duas, uma superfície S e outra S 1 (esfera adicionada)...

∬ S   F → ⋅ d S → + ∬ S 1   F → ⋅ d S → = ∭ W   d i v   F → d V

Se queremos a integral sobre S , a isolemos...

∬ S   F → ⋅ d S → = ∭ W   d i v   F → d V - ∬ S 1   F → ⋅ d S →

Podemos simplificar mais ainda se você inverter o sinal da integral em S 1 mas invertendo o sentido do vetor normal a ela, ou seja, ao invés de entrar, ele sai:

∬ S   F → ⋅ d S → = ∭ W   d i v   F → d V + ∬ S 1   F → ⋅ d S →

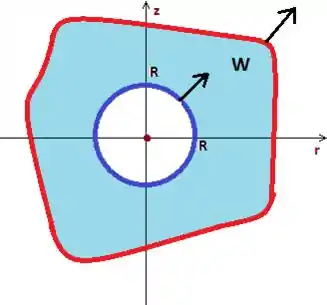
Passo 6

Vamos começar com a integral tripla, mas repare que ainda nos falta calcular o divergente:

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z

Como

F → x ,   y ,   z = x x 2 + y 2 + z 2 3 2 ⏟ F 1 ,   y x 2 + y 2 + z 2 3 2 ⏟ F 2 ,   z x 2 + y 2 + z 2 3 2 ⏟ F 3   →

Calculando a primeira derivada parcial com atenção na regra da fração e na da cadeia...

∂ F 1 ∂ x = ∂ ∂ x x x 2 + y 2 + z 2 3 2 =

x 2 + y 2 + z 2 3 2 ⋅ ∂ ∂ x x - x ⋅ ∂ ∂ x x 2 + y 2 + z 2 3 2 x 2 + y 2 + z 2 3 2 2 =

x 2 + y 2 + z 2 3 2 - 3 2 x ⋅ x 2 + y 2 + z 2 1 2 ⋅ 2 x x 2 + y 2 + z 2 3 =

x 2 + y 2 + z 2 3 2 - 3 x 2 x 2 + y 2 + z 2 1 2 x 2 + y 2 + z 2 3

Essa é só uma derivada, a da F 1 com relação à x . Mas, como as demais são simétricas a ela encontramos por inspeção que...

∂ F 2 ∂ y = x 2 + y 2 + z 2 3 2 - 3 y 2 x 2 + y 2 + z 2 1 2 x 2 + y 2 + z 2 3

∂ F 3 ∂ z = x 2 + y 2 + z 2 3 2 - 3 z 2 x 2 + y 2 + z 2 1 2 x 2 + y 2 + z 2 3

Juntando todas elas em uma soma grandinha, então cuidado pra não errar nada...

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z   →

d i v   F → = x 2 + y 2 + z 2 3 2 - 3 x 2 x 2 + y 2 + z 2 1 2 x 2 + y 2 + z 2 3 + x 2 + y 2 + z 2 3 2 - 3 y 2 x 2 + y 2 + z 2 1 2 x 2 + y 2 + z 2 3 + x 2 + y 2 + z 2 3 2 - 3 z 2 x 2 + y 2 + z 2 1 2 x 2 + y 2 + z 2 3     →

d i v   F → = x 2 + y 2 + z 2 3 2 - 3 x 2 x 2 + y 2 + z 2 1 2 + x 2 + y 2 + z 2 3 2 - 3 y 2 x 2 + y 2 + z 2 1 2 + x 2 + y 2 + z 2 3 2 - 3 z 2 x 2 + y 2 + z 2 1 2 x 2 + y 2 + z 2 3 →

d i v   F → = 3 x 2 + y 2 + z 2 3 2 - 3 x 2 + y 2 + z 2 1 2 x 2 + y 2 + z 2 x 2 + y 2 + z 2 3     →

d i v   F → = 3 x 2 + y 2 + z 2 3 2 - 3 x 2 + y 2 + z 2 3 2 x 2 + y 2 + z 2 3     →

d i v   F → = 0

HÁ! Essa conta imensa pra dar zero depois. Que ótimo não?

Passo 7

Calculando agora a integral de superfície sobre a esfera...

∬ S 1   F → ⋅ d S →

Precisamos primeiro parametrizar S 1 . Como é uma esfera:

x = R sin ⁡ φ cos ⁡ θ

y = R sin ⁡ φ sin ⁡ θ

z = R cos ⁡ φ

Lembre-se que de que R é o raio da esfera, um número e não uma variável. Então pela parametrização fica...

σ θ ,   φ = R sin ⁡ φ cos ⁡ θ , R sin ⁡ φ sin ⁡ θ ,   R cos ⁡ φ

Onde φ e θ são...

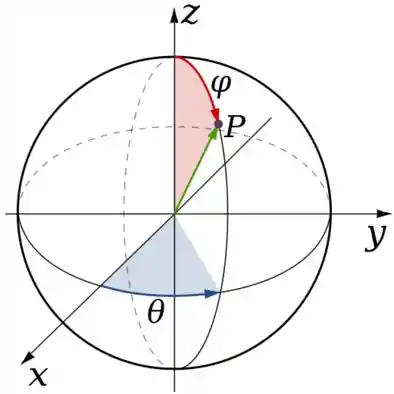
Logo, por comparação com a superfície S 2 ...

0 ≤ θ ≤ 2 π

0 ≤ φ ≤ π

Passo 8

Devemos agora substituir os termos da parametrização na função

F → x ,   y ,   z = x x 2 + y 2 + z 2 3 2 ,   y x 2 + y 2 + z 2 3 2 ,   z x 2 + y 2 + z 2 3 2    

Lembre-se que pela equação da esfera, nem precisamos substituir o denominador, pois x 2 + y 2 + z 2 = R 2 ...

F → x ,   y ,   z = x R 2 3 2 ,   y R 2 3 2 ,   z R 2 3 2 →

F → σ θ ,   φ = R sin ⁡ φ cos ⁡ θ R 2 3 2 ,   R sin ⁡ φ sin ⁡ θ R 2 3 2 ,   R cos ⁡ φ R 2 3 2 →

F → σ θ ,   φ = R sin ⁡ φ cos ⁡ θ R 3 ,   R sin ⁡ φ sin ⁡ θ R 3 ,   R cos ⁡ φ R 3     →

F → σ θ ,   φ = sin ⁡ φ cos ⁡ θ R 2 ,   sin ⁡ φ sin ⁡ θ R 2 ,   cos ⁡ φ R 2    

Passo 9

Quanto ao termo d S → que temos de encontrar, bem você pode jogar pela fórmula:

d S → = N → d θ d φ

Onde

N → = ∂ σ θ ,   φ ∂ θ × ∂ σ θ ,   φ ∂ φ

Ou, basta aplicar o bizu de vetor normal de superfícies esféricas:

N → = R sin ⁡ φ σ θ ,   φ = R sin ⁡ φ R sin ⁡ φ cos ⁡ θ , R sin ⁡ φ sin ⁡ θ ,   R cos ⁡ φ   →

R 2 sin 2 ⁡ φ cos ⁡ θ , R 2 sin 2 ⁡ φ sin ⁡ θ ,   R 2 sin ⁡ φ cos ⁡ φ

Note que esse vetor satisfaz a condição de estar pra fora da esfera.

Passo 10

Retornando à integral de superfície:

∬ S 1   F → ⋅ d S → =

E substituindo os caras:

∫ 0 2 π ∫ 0 π sin ⁡ φ cos ⁡ θ R 2 ,   sin ⁡ φ sin ⁡ θ R 2 ,   cos ⁡ φ R 2 ⋅ R 2 sin 2 ⁡ φ cos ⁡ θ , R 2 sin 2 ⁡ φ sin ⁡ θ ,   R 2 sin ⁡ φ cos ⁡ φ d φ d θ =

∫ 0 2 π ∫ 0 π sin 3 ⁡ φ cos 2 ⁡ θ +   sin 3 ⁡ φ sin 2 ⁡ θ + sin ⁡ φ cos 2 ⁡ φ   d φ d θ =

∫ 0 2 π ∫ 0 π sin 3 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ + sin ⁡ φ cos 2 ⁡ φ   d φ d θ =

∫ 0 2 π ∫ 0 π sin 3 ⁡ φ + sin ⁡ φ cos 2 ⁡ φ   d φ d θ =

∫ 0 2 π ∫ 0 π sin ⁡ φ sin 2 ⁡ φ + cos 2 ⁡ φ   d φ d θ =

∫ 0 2 π ∫ 0 π sin ⁡ φ   d φ d θ =

∫ 0 2 π - c o s φ 0 π   d θ = 2 θ 0 2 π = 4 π

Então pelo Teorema de Gauss...

∬ S   F → ⋅ d S → = ∭ W   d i v   F → d V + ∬ S 1   F → ⋅ d S →

∬ S   F → ⋅ d S → = 4 π

Resposta

4 π