Considere dois cilindros longos de materiais diferentes onde um cilindro é encaixado dentro do outro. O raio interno do cilindro interno é e o raio externo, . O raio interno do cilindro externo também é e seu raio externo é . O módulo de Young e o coeficiente de Poisson do cilindro interno são e , respectivamente, e os do cilindro externo são e , respectivamente. A tensão radial , a tensão circunferencial , e o deslocamento radial são dados por:
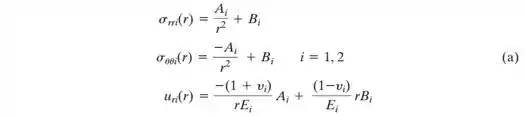
Onde se refere ao cilindro interno e , ao cilindro externo.
Se a superfície externa do cilindro externo é submetida a um deslocamento radial compressivo e a superfície interna do cilindro interno não tem tensões radiais, então as seguintes quatro condições de contorno podem ser usadas para determinar e , :
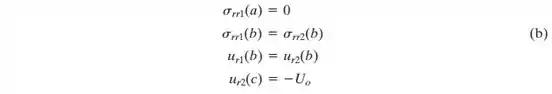
Substituindo as Equações (a) em (b) , o seguinte sistema de equações na forma matricial é obtido:

Determine a tensão circunferencial nos cilindros interno e externo em , considerando , , , , , e .
Passo 1
O enunciado nos dá um sistema de equações lineares na forma matricial, com quatro equações e quatro incógnitas, cuja solução nos dará as constantes , , e , necessárias para o cálculo da tensão circunferencial , dada pela equação:
![]()
O exercício pede para calcular a tensão circunferencial nos cilindros interno e externo em . Para isto, primeiro resolveremos o sistema de equações lineares para obter , , e , usando uma das funções que vimos para resolver sistemas de equações lineares no MATLAB: matriz inversa, barra invertida, ou o .
Com a solução do sistema de equações, podemos calcular a tensão circunferencial de cada cilindro, usando a equação acima e considerando . O cilindro interno é dado por , logo, para calcular sua tensão circunferencial, usaremos e . Já para o cilindro externo, e usaremos e para determinar sua tensão circunferencial.
Passo 2
O sistema de equações lineares no enunciado está no formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas , , e e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita. Logo, pelo enunciado, temos:
Em um script novo no MATLAB, entre com os dados fornecidos pelo enunciado: os coeficientes de Poisson (representados abaixo por e ), os módulos de Young (representados abaixo por e ), o deslocamento radial compressivo (indicado por abaixo) e os raios , e :
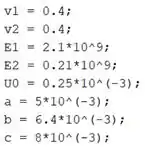
Note que o deslocamento radial e os raios , e foram convertidos de para por meio da multiplicação por . Fazemos isso porque a unidade do módulo de Young está em e para que a unidade da tensão que calcularemos no final também seja em .
Em seguida, entre com a matriz e o vetor :
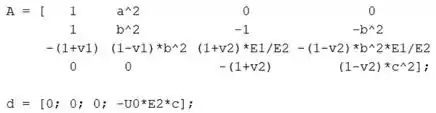
Passo 3
Após definir e , podemos resolver o sistema de equações e encontrar o vetor , representando a solução do sistema.
Vimos quatro formas de resolver um sistema linear no MATLAB: inversão de matriz , barra invertida, e . Você pode usar a forma que quiser, eu escolhi usar a barra invertida:
![]()
Qualquer uma das formas retornará o mesmo vetor . Rode seu programa e ele calculará o vetor como:

Passo 4
Os elementos de são as constantes , , e que servem para calcular a tensão circunferencial , dada pela equação:
![]()
Para facilitar a implementação da equação de para os dois cilindros, vamos armazenar os elementos de em variáveis designando as constantes , , e , por meio das linhas de código:

Na primeira linha, armazenamos o primeiro elemento de na variável , representando a incógnita . Na segunda linha, armazenamos o segundo elemento de na variável , representando a incógnita . e são usados para calcular a tensão circunferencial do cilindro interno.
Na terceira linha, armazenamos o terceiro elemento de na variável , representando a incógnita . Na quarta linha, armazenamos o quarto elemento de na variável , representando a incógnita . e são usados para calcular a tensão circunferencial do cilindro externo.
Tendo feito essas definições, podemos implementar em nosso código a equação que calcula a tensão circunferencial dos dois cilindros, por meio das linhas de código:

Na primeira linha, dizemos que , pois o enunciado pediu que calculássemos a tensão circunferencial nesse valor de raio.
Na segunda linha, calculamos a tensão circunferencial do cilindro interno, designado por , usando a equação de . O resultado é armazenado em .
Na terceira linha, calculamos a tensão circunferencial do cilindro externo, designado por , também usando a equação de . O resultado é armazenado em .
Ao executar o programa, você terá e , que são as tensões circunferenciais nos cilindros interno e externo em :

Resposta
A tensão circunferencial no cilindro interno é:
A tensão circunferencial no cilindro externo é: