Considere o sistema linear:
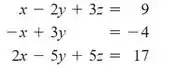
- Use o comando do MATLAB para resolver o sistema;
- Seja a matriz de coeficientes do sistema, e o lado direito das equações:

Use o comando do MATLAB para resolver o sistema.
Passo 1
O exercício nos dá um sistema de equações lineares de 3 equações com 3 incógnitas. Na letra a, ele nos pede para resolver o sistema usando a função , que dá a forma escalonada reduzida de uma matriz.
Para resolver um sistema de equações lineares usando , temos que passar o sistema para o formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas (no caso, , e ) e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita.
Com a matriz de coeficientes e o vetor , construímos a matriz aumentada . É a matriz aumentada que vai ser escalonada com o , e é a partir da análise de sua forma escalonada reduzida que encontramos uma solução para o sistem linear de equações.
A letra b nos dá a matriz de coeficientes A e o vetor B e pede para resolvermos o mesmo sistema de equações lineares de outra forma: usando a divisão de matrizes, ou seja, a barra invertida ().
Este exercício é legal porque podemos praticar duas formas diferentes de resolver o sistema e comparar os resultados.
Passo 2
Vamos resolver a letra a. A primeira coisa a fazer é criar um script novo no MATLAB e entrar com a matriz de coeficientes e o vetor , que nos são dados na letra b do exercício:
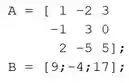
Em seguida, vamos construir a matriz aumentada , usando a linha de código:
![]()
Este comando cria uma nova matriz que é uma junção da matriz com o vetor . Basicamente, adicionamos mais uma coluna à , correspondendo a . Fica melhor de visualizar se pedirmos ao MATLAB para imprimir a matriz aumentada :

Repare que as três primeiras colunas de são a matriz e a última coluna, o vetor .
Passo 3
É com a matriz aumentada que encontraremos a solução do sistema linear, usando-a como entrada da função . No seu script do MATLAB, adicione a linha de código:
![]()
Esta linha de código cria a forma escalonada reduzida de , por meio do , e a armazena na variável .
A solução do sistema de equações está na matriz . Rode seu programa e peça ao MATLAB para imprimi-la no Command Window:

Perceba que as três primeiras colunas de compõem uma matriz identidade . Isto quer dizer que nosso sistema de equações, com equações e incógnitas, tem solução única. Esta solução única está na quarta coluna de .
Podemos voltar ao formato de sistema de equações partindo de . Este processo nos dará a solução do sistema linear, pois teremos:
Pronto! Esta é a solução do sistema. Letra a respondida ;D
Passo 4
Vamos responder à letra b do exercício. Ela pede para resolvermos o mesmo sistema de equações, mas usando divisão de matrizes.
Vamos resolver a letra b no mesmo script onde fizemos a letra a. Como já entramos com a matriz de coeficientes e o vetor , basta adicionarmos a seguinte linha de código para respondermos a letra b:
![]()
O comando calculará a solução do sistema de equações e armazenará o resultado no vetor .
Vamos rodar o programa e pedir ao MATLAB para nos mostrar :
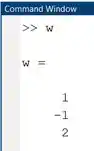
Repare que é igualzinho à quarta coluna de . Logo, chegamos ao mesmo resultado usando e .
Resposta
- A solução do sistema, usando , é:
- A solução do sistema linear de equações, usando , é: