A figura abaixo mostra uma massa suspensa por três cabos presos em três pontos B, C e D.
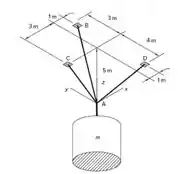
As tensões nos cabos AB, AC e AD são representadas por , e , respectivamente. Se a massa está em equilíbrio estático, a soma dos componentes das tensões nas direções , e deve ser igual a . Isso resulta nas seguintes três equações:
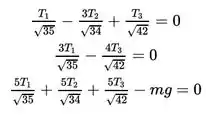
Determine , e . Considere e .
Passo 1
O exercício nos dá um um sistema de equações lineares, com três equações e três incógnitas. As incógnitas são , e .
O enunciado pede para solucionarmos o sistema linear, isto é, encontrarmos os valores de , e . Para isto, usaremos uma das funções que vimos para resolver sistemas de equações lineares no MATLAB: matriz inversa, barra invertida, ou o .
Passo 2
Primeiramente, vamos passar o sistema de equações lineares para o formato matricial:
Onde é uma matriz com os coeficientes das equações, é o vetor com as incógnitas , e e é o vetor com os valores numéricos à direita do sinal de igual, que não são multiplicados por nenhuma incógnita.
Para colocarmos o sistema no formato matricial, temos que dar uma manipuladinha na terceira equação do sistema, jogando à direita da igualdade:
Logo, este é o nosso sistema de equações:
No formato matricial, temos:
Agora, crie um script novo no MATLAB, entre com a massa , a aceleração da gravidade , a matriz e o vetor :

Passo 3
Após entrar com e , podemos resolver o sistema de equações e encontrar o vetor , representando a solução do sistema.
Vimos quatro formas de resolver um sistema linear no MATLAB: inversão de matriz , barra invertida, e . Para resolver este exercício, recomendo utilizar qualquer uma das três primeiras opções, menos a , pois vamos praticar seu uso em outros exercícios mais pra frente. Mas caso queira usar a , não esqueça de construir a matriz aumentada .
Forma 1: inversa da matriz
Caso queira usar a inversão da matriz para resolver o sistema, digite no script a linha de código:
![]()
Forma 2: barra invertida (divisão de matrizes)
Caso queira usar a barra invertida para resolver o sistema, digite a linha de código:
![]()
Forma 3:
Caso queira usar a função para resolver o sistema, digite a linha de código:
![]()
Qualquer uma das três formas retornará o mesmo vetor . Rode seu programa e ele calculará o vetor como:
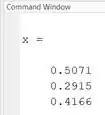
Isto significa que a solução do sistema de equações lineares é , e .
Resposta
As tensões nos cabos AB, AC e AD são , e , respectivamente