Para o circuito abaixo, determine quando e :
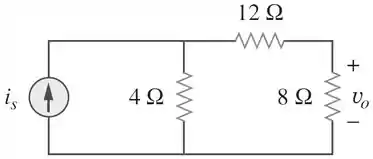
Passo 1
Antes da gente começar a usar a Superposição, precisamos entender bem essa ferramenta poderosa que se chama Linearidade! Então vamos esquentar nossos motores com essa questão que é bem simples.
Nessa questão precisamos achar uma relação entre e , para verificarmos a relação de linearidade do circuito.
Passo 2
Para isso, vamos utilizar o método de análise nodal:
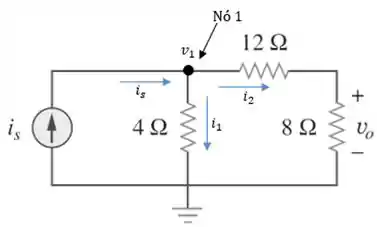
Aplicando LCK no nó 1, a equação das correntes fica assim:
Passo 3
Escrevendo as correntes em função da tensão nodal :
Passo 4
Substituindo na equação das corretes:
Passo 5
Agora, vamos utilizar divisor de tensão para calcular a tensão :
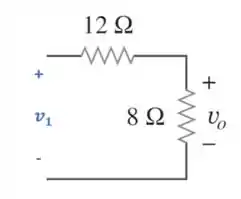
Substituindo :
Passo 6
Quando , temos:
Quando , temos:
Esses resultados comprovam a relação de linearidade, pois quando a fonte de corrente teve seu valor multiplicado por , o também foi multiplicado pelo mesmo valor.
Resposta
e