Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Superposição

Ver Teoria
Exercício 61234578910

Enunciado

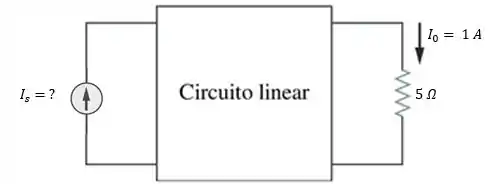
Supondo I 0 = 1   A e usando a propriedade da linearidade, encontre o valor real de I 0 no circuito abaixo:

Passo 1

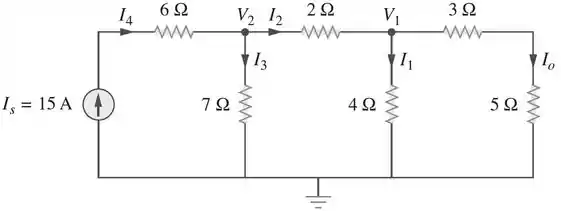
Nesse problema ele quer saber quanto de corrente a fonte tem que fornecer para que no resistor de 5 Ω consiga “chegar” 1A. Sendo assim, vamos encontrar o valor de entrada da fonte de corrente que produz essa saída, conforme o esquema abaixo:

Passo 2

Como circuito já está preparado para ser feito por análise nodal:

Se I 0 = 1   A :

V 1 = 3 + 5 I 0 = 8   V

Como V 1 = 8   V :

I 1 = V 1 4 = 8 4 = 2   A

Passo 3

Aplicando LCK no nó de V 1 :

I 2 = I 1 + I 0

Substituindo:

I 2 = 2 + 1 = 3   A

Como,

I 2 = V 2 - V 1 2

Substituindo: V 1 = 8   V e I 2 = 3   A :

V 2 = 14   V

Passo 4

Como tem-se que:

I 3 = V 2 7

Substituindo V 2 :

I 3 = 14 7 = 2   A

Passo 5

Agora, vamos aplicar a LCK no nó de V 2 :

I 4 = I 2 + I 3

Substituindo:

I 4 = 3 + 2 = 5   A

Como I 4 é o próprio I s :

I s = 5   A

Isso mostra que supondo I 0 = 1   A obteremos uma entrada I s = 5   A . Logo, utilizando a propriedade da linearidade, quando a entrada for o valor real da fonte de corrente, ou seja, I s = 15   A , a saída I 0 resultará no valor real de 3   A .

I 0 = 1   A       →       I s = 5   A

Multiplicando por três:

I 0 = 3   A       →       I s = 15   A

Resposta

I 0 = 3   A

Exercícios de Livros Relacionados

10. Usando a figura 4.78 elabore um problema para ajudar outros estudantes a entenderem melhor o teorema da superposição. Note que a letra k é um ganho que você pode especificar de forma a tornar o pr
8. Usando a superposição, determine V 0 no circuito da Figura 4.76 . Confira usando o P s p i c e ou o M u l t i S i m .
9. Dado que I = 4A quando V s = 40V e I s = 4A e I = 1A quando V s = 20V e I s = 0A , use o teorema da superposição e linearidade para determinar o valor de I quando V s = 60V e I s = - 2A .
14. Aplique o princípio da superposição para determinar v 0 no circuito da figura 4.82
16. Dado o circuito da figura 4.84 , use superposição para obter i 0 .