Uma bolinha de experimenta, por um breve intervalo de tempo, uma enorma aceleração (módulo) de ordem , devido ao impacto da mesma com uma parede. Esta aceleração inverta a direção (ou sentido) da velocidade da bolinha durante o curto intervalo de tempo do impacto. Sobre os módulos da força e aceleração experimentadas pela parede devido a este processo, podemos afirmar:
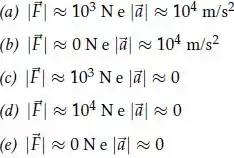
Passo 1
Como ele fala a aceleração da bolinha pra gente vamos chamar o noss amigo Nenê para aplicar a segunda lei dele aqui
Passo 2
Ainda usando o nosso amigo Newton, vamos pegar a terceira lei dele (ação e reação).
Como a parede faz uma força de na bolinha, a bolinha também faz a mesma força na parede, mas convenhamos que nenhuma bolinha vai movimentar a parede, né? A massa da parede é muuuuuuuuito maior que a massa da bolinha!