Cada uma das figuras abaixo mostra blocos de massa e , atuados por uma força horizontal externa . Para cada figura, qual das seguintes afirmações a respeito da força que cada bloco exerce sobre o outro é verdadeira? Despreze todos os atritos.
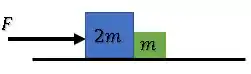
Figura 1
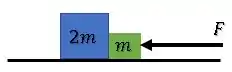
Figura 2
A. e
B. e
C. e
D. e
E. e
Passo 1
Bom, as situações parecem idênticas, né?
Então a força entre os blocos é igual para os dois casos, né?
Nãooo! Muito cuidado aqui.

Vamos analisar cada caso para ver a diferença.
Passo 2
Na primeira situação, temos:
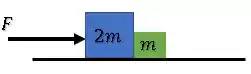
Concorda comigo que esses blocos vão sempre andar juntos?
Então, eles vão ter a mesma aceleração .
Assim, podemos considerar os dois blocos como um blocão só de massa igual à soma das duas massas e .
Aplicando a Segunda Lei de Newton, temos:
Ou seja, essa será a aceleração tanto do bloco azul quanto do bloco verde.
Passo 3
Agora que temos a aceleração dos blocos, podemos analisar apenas um deles e aplicar novamente a Segunda Lei de Newton, para encontrar a força entre eles.
Se pegarmos, por exemplo o bloco verde, apenas a força de contato entre eles estará empurrando esse bloco:
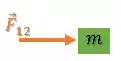
Substituindo a aceleração que encontramos, temos:
Esse será o módulo da força de que o bloco azul exerce sobre o verde, que vale o mesmo que a força que o bloco verde exerce sobre o bloco azul.
Passo 4
Já na segunda situação, temos:
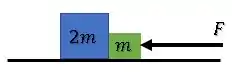
Repara que a Segunda Lei de Newton para o nosso blocão ficará a mesma, considerando o sentido positivo agora para a esquerda:
Então, achamos um mesmo valor de aceleração para o bloco azul e o verde.
Isso faz sentido, já que a força externa atuando sobre eles é a mesma.
Entretanto, nesse segundo caso, o bloco verde estará empurrando o bloco azul (mais pesado). Assim, a força de contato entre eles será maior.
Vamos fazer a conta e checar isso...
Passo 5
Aplicando a Segunda Lei de Newton apenas para o bloco azul, agora, temos:
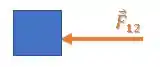
Substituindo o valor de aceleração:
Essa será a força de contato entre os blocos na segunda situação.
Assim, ficamos com na primeira e na segunda. Marcamos a letra C.
Resposta
Letra (C)