Preencha cada campo com sua resposta.
Dois blocos em forma de cubo, de massas e , estão sobre um piso horizontal sem atrito, encostados um ao outro. Uma força horizontal de módulo é aplicada sobre , em direção a .
O módulo da força de contato entre e é .
Passo 1
Vamos tentar enxergar a situação. Nós temos dois blocos (um menorzinho, com e outra maior com ) encostados um no outro.
Então é aplicada uma força horizontal no bloquinho , em direção a .
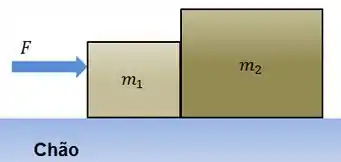
Queremos saber o módulo da força de contato que vai fazer em e, pela terceira lei de Newton, vai fazer em .
Passo 2
Agora que já visualizamos o problema, vamos separá-lo em duas partes: As forças que atuam em e as que atuam em .
Em temos a força e a força de contato que realiza, ambas horizontais mas com sentidos opostos. A força resultante vai ser
Pela segunda lei de newton, teremos:
No bloquinho , teremos apenas a força de contato. Isso nos dá:
Novamente:
Passo 3
Falta uma última coisa nas equações anteriores: A aceleração das duas caixas tem que ser igual.
Se a aceleração da caixa fosse maior, ela iria atravessar a caixa 2 (?!), porque se moveria mais rápido com o tempo. Isso é impossível, a não ser que ela fosse um fantasma.
Se a aceleração da caixa 2 fosse maior, uma hora ela iria estar mais rápida que a caixa , e elas não andariam mais juntas. Isso seria possível, mas seria confuso.
Quando as duas se soltassem, a caixa 2 não teria mais aceleração, enquanto a caixa 1 teria, e logo elas colidiriam depois de um tempo. Aí o que ia acontecer?
Vamos adicionar essa informação nas equações anteriores:
Juntando as duas, podemos achar a aceleração do nosso sistema:
Substituindo na força de contato:
Observação:
A equação é basicamente a segunda lei de newton se considerássemos os dois bloquinhos como um grande blocão.
Nesse caso, forças internas não entrariam na conta da força resultante (por causa da ação e reação) e a força resultante seria exatamente .
Poderíamos ter raciocinado assim mas ainda precisaríamos olhar cada caixa separadamente porque é exatamente a força interna que queremos calcular!
Resposta
O módulo da força de contato entre e é .