Dois blocos ( e ) estão em contato sobre uma superfície horizontal sem atrito. Uma força constante de é aplicada ao bloco , como mostra a figura abaixo. O módulo da força que exerce sobre é:
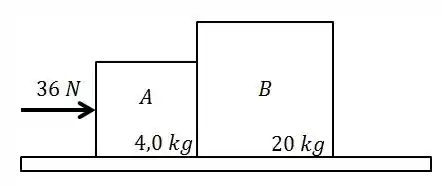
A.
B.
C.
D. 30
E. 36
Passo 1
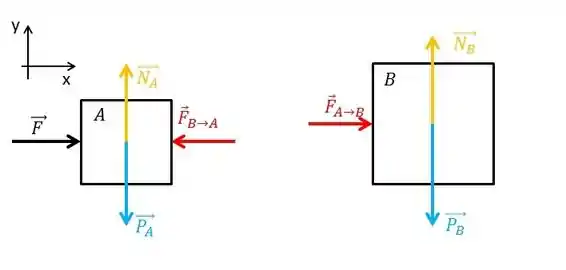
Vamos desenhar todas as forças que agem nos dois corpos pra gente poder achar a força que A faz em B,
Beleza, temos o peso e a normal nos dois corpos, já que eles estão sofrendo a atração da Terra, e porque eles estão apoiados numa superfície.
O corpo A tá sofrendo essa força de , vamos chamar ela de , ok?
E, bem, o corpo A empurra o corpo B para a direita, consequentemente, o corpo B empurra o corpo A para a direita. Pensa que você tá andando e dá uma topada com o dedinho no canto da mesa, então, a força que o seu dedinho sofreu, a mesa também sofreu. Esse é o nosso famoso par ação-reação. As forças tem o mesmo módulo, mas sentidos opostos e atuam em corpos diferentes!
Passo 2
Não temos nenhum movimento na vertical, então podemos dizer que a para ambos os corpos. Então vamos direto analisar as forças na horizontal.
Usando a segunda lei de Newton para o corpo A:
Lembra que eu falei, do par ação e reação, eles tem o mesmo módulo:
Show? Então, vamos reescrever a equação de cima:
Estamos chegando perto! Queremos saber quem é , então vamos isolar ela:
Maravilha! Agora o que falta pra gente achar é a , pra isso vamos usar a segunda lei de newton de novo, mas agora vai ser no corpo B:
Passo 3
Para o corpo B, pela segunda lei de Newton:
Vamos isolar o nessa equação e substituir lá na última equação do passo anterior:
Acompanha comigo:
Então, como tínhamos:
Substituindo o :
Resolvendo essa continha:
Show??
Resposta
Alternativa D.