Uma máquina A produz peças circulares cujos diâmetros devem obedecer a uma determinada especificação em , e uma outra máquina B foi encontrada no mercado. Quer-se saber se os diâmetros médios das duas máquinas são semelhantes, ou seja, se as máquinas produzem peças que podem ser consideradas estatisticamente iguais em termos dos diâmetros delas.

Tomou-se uma amostra de peças da máquina A e peças da máquina B, tendo sido obtidas as seguintes estimativas amostrais:

Máquina A: e ;

Máquina B: e ;

a) Teste a hipótese se existe diferença entre a média dos diâmetros da máquina A () para a média dos diâmetros da máquina B (), ao nível de significância de .

b) Através do teste de hipótese para a variância, determine com o nível de significância de se existe diferença entre a variância dos gastos da máquina A () para a variância dos gastos da máquina B ().

Um gráfico da distribuição é dado a seguir:

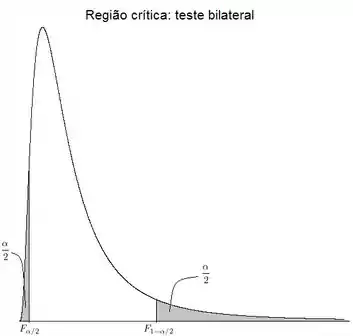
Como o teste é bilateral, a porcentagem da região central deve ser , de modo que dividimos para cada extremidade. Temos que calcular e .

Temos que

Recorremos à tabela:

Portanto,

Já para o mínimo, temos

A prova não forneceu a tabela para a distribuição com . Mas olhando para a distribuição podemos perceber que deve ser muito pequeno, bem menor que . Isso que vai nos importar como vou te mostrar no próximo passo!

Agora calculamos supondo que (isso que queremos verificar no nosso teste):

Para que a hipótese seja aceita e as variâncias sejam compatíveis, devemos ter . Como , temos que . Resta ver se , o que é bem simples.

Apesar de não termos achado , concluímos que deve ser um número bem pequeno, menor que . Com isso, a condição é garantida. Portanto, as variâncias são compatíveis entre si!

Pronto! Finalizamos a questão 😉!

Até a próxima!