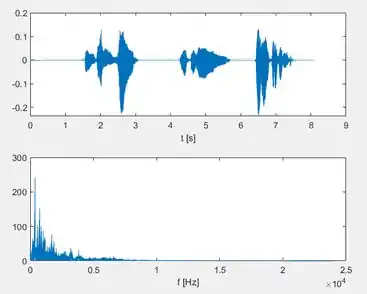
Neste exercício, você encontrará o conteúdo de espectro e frequência do seu próprio sinal de voz.

1. Vá ao site https://online-voice-recorder.com/pt/ e grave uma fala sua. Você pode dizer o que quiser ou ler a frase abaixo:

“No Responde Aí, é como se você estivesse estudando do lado daquele amigo que sabe tudo.”

2. Escute ao sinal do seu áudio e então leia-o no MATLAB usando a função .
3. Determine o espectro de frequência do sinal de voz.
4. Plote o sinal no domínio do tempo e no domínio da frequência no mesmo gráfico, como na figura abaixo:

Vamos começar pela letra a. Vamos no site recomendado pelo enunciado para gravarmos nossa voz. Ao abrir o site no navegador, você verá que tem um botão vermelho (indicado pela seta na figura abaixo), no qual você deve clicar para iniciar a gravação:

Ao iniciar a gravação, fale a frase que desejar ou a sugerida pelo enunciado. Para encerrar a gravação, aperte o botão de “Stop” no site (destacado abaixo).

Você pode escutar sua gravação antes de salvar o áudio em formato mp3, clicando no botão destacado abaixo.

Salve o áudio na pasta onde você salvará o script do MATLAB onde você escreverá o código deste exercício.

Feita a letra a, vamos fazer a letra b. Primeiro, escute o áudio que você gravou. Não se preocupe, eu te espero.

Em seguida, crie um script novo no MATLAB, salve-o na pasta onde você salvou a gravação da sua voz e digite o comando:

Esta é a função do MATLAB. Ela lê arquivos de áudio e tem como entrada um string do nome do arquivo de áudio a ser lido. No meu caso, eu salvei a gravação da minha voz como minha_voz.mp3, por isso a entrada do comando acima é . Lembre-se de alterar para o nome do seu arquivo de áudio.

A função retorna duas saídas: o vetor , que é o sinal do áudio do arquivo de entrada no domínio do tempo, e a frequência de amostragem do sinal.

Tendo concluído a letra b, vamos para a letra c.

Na letra , temos que determinar o espectro de frequência do sinal de voz, isto é, analisá-la no domínio da frequência. Para isto, usaremos a função do MATLAB no vetor , obtido no passo 3, que converte sinais no domínio do tempo para o domínio da frequência.

Digite em seu script o comando:

A função tem como entrada o vetor , que contém números reais representando o sinal da gravação da nossa voz no domínio do tempo. Já a saída é um vetor com números complexos: é a conversão de no domínio do tempo para o domínio da frequência. Os vetores e têm a mesma quantidade de elementos.

O vetor é o espectro de frequência do sinal de voz, logo, a letra c está concluída.

Vamos resolver a letra d, que pede pra plotarmos, em um mesmo gráfico, o sinal da nossa voz no domínio do tempo e no domínio da frequência.

Vamos começar gerando as informações para plotar o sinal no domínio do tempo. Precisamos criar um vetor que representará o domínio do tempo, em segundos, e será o eixo X do gráfico do sinal no domínio do tempo. O vetor será criado a partir do comando:

Neste comando, cria-se primeiro um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos medidos na nossa gravação de voz. Em seguida, esse vetor é multiplicado por , que é o período, em segundos, do sinal.

Precisamos, então, primeiro determinar e antes de calcular o vetor .

Como é o número de pontos medidos, ele corresponde ao número de elementos do vetor , que é o sinal de áudio no domínio do tempo. Logo, para obter, podemos fazer , pois a função retorna a quantidade de elementos de um vetor.

O período do sinal é o inverso da frequência de amostragem , isto é, . A frequência de amostragem foi obtida no passo 3, com o .

Logo, adicione em seu script os seguintes comandos para criar o vetor representando o domínio do tempo:

Por curiosidade: se você rodar o programa que digitou até agora e pedir ao MATLAB para ver o último elemento do vetor , com o comando , no Command Window, você verá que ele corresponde à duração da gravação do seu áudio, em segundos. No meu caso, minha gravação tinha um pouco mais de segundos:

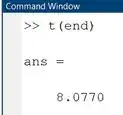
Com os vetores e , conseguimos plotar o sinal da nossa voz no domínio do tempo.

Agora, vamos gerar as informações para plotar o espectro de frequência da gravação da nossa voz, isto é, o sinal de nossa voz no domínio da frequência.

Quando plotamos um sinal no domínio da frequência, normalmente temos no eixo vertical do gráfico a magnitude do sinal obtido pela função . Para calcular a magnitude, usamos a função do MATLAB. Digite no MATLAB a linha de código:

Com esta linha, calculamos a magnitude de cada elemento do vetor usando a função do MATLAB. Quando a entrada da função é um número complexo, ela calcula sua magnitude.

Agora precisamos criar o eixo horizontal do gráfico, representando o domínio da frequência. Para isto, digite os comandos:

Na primeira linha, calculamos o , que é o passo do domínio da frequência: ele começa em e as frequências seguintes são obtidas pela soma de à frequência anterior. O é calculado dividindo a frequência de amostragem pelo número de pontos e é armazenado na variável .

Na segunda linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.

Primeiramente, cria-se um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos capturados do sinal da nossa gravação. Em seguida, esse vetor é multiplicado por . Desta forma, é criado o domínio da frequência, que vai de a

Com os vetores e , conseguimos plotar o sinal da nossa voz no domínio da frequência.

Pra gerar o gráfico pedido na letra d, usaremos o comando do MATLAB.

Digite em seu script as seguintes linhas de código para gerar o gráfico:

Na primeira linha, com o comando , pedimos ao MATLAB para dividir a janela onde serão gerados os gráficos em uma “tabela” de duas linhas e uma coluna. Em seguida, indicamos que vamos plotar o gráfico da primeira linha da “tabela”.

Na segunda linha, com o comando o gráfico do sinal da nossa voz no domínio do tempo é gerado.

Na terceira linha, indicamos que o eixo horizontal do gráfico é o domínio do tempo por meio do comando .

Na quarta linha, indicamos que vamos plotar o segundo gráfico, na segunda linha da “tabela” criada pelo .

Em seguida, na quinta linha, o gráfico da magnitude de no domínio da frequência é criado com o comando Repare que, para plotar, usamos somente a primeira metade dos vetores com elementos e . Isso é indicado pela adição de à direita do nome do vetor, que diz ao MATLAB que queremos pegar do primeiro elemento ao elemento do vetor.

Usamos somente a primeira metade dos vetores e porque, no domínio da frequência, a partir de , as magnitudes começam a se repetir e não precisamos pôr elas no gráfico.

Finalmente, na última linha, indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando .

Ao executar o programa, teremos o gráfico pedido na letra d.