Uma propriedade da Transformada de Fourier é que a transformada da convolução de duas funções equivale à multiplicação das duas no domínio da freqüência. Portanto, para calcular a convolução de uma função levamos os dois sinais para o domínio da freqüência, os multiplicamos e voltamos para o domínio do tempo.
Digamos que você queira calcular a convolução das funções e . Você pode fazer isso da seguinte maneira:
Considerando essa propriedade, calcule a convolução das formas de onda:
e
Passo 1
Neste exercício, vamos usar o comando e (comando novo que vamos aprender aqui!) para calcular . No nosso programa, vamos primeiramente entrar com e no domínio do tempo. Em seguida, aplicaremos em e a função do MATLAB para calcular as funções no domínio da frequência e então multiplicaremos os resultados entre si.
No resultado da multiplicação, vamos usar a função do MATLAB , que calcula a inversa da transformada de Fourier, para voltar ao domínio do tempo. A saída de é a convolução de e e a solução do exercício.
Passo 2
Em um script novo, vamos criar um vetor representando o domínio do tempo e, em seguida, entrar com e :

Na primeira linha, criamos o vetor , que vai de a , com um passo de .
Na segunda e na terceira linha, calculamos e para cada elemento do vetor . Os resultados são armazenados nos vetores e , respectivamente. Portanto, os vetores e representam e em um domínio de tempo .
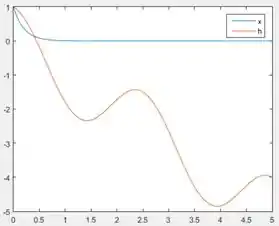
Para ver a cara de e plotando suas curvas em um mesmo gráfico, digite os comandos abaixo:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico de e em uma janela diferente do gráfico do resultado da convolução (que será gerado mais pra frente). Em seguida, com o comando as curvas de em função de e em função de são geradas.
O comando fará com que o gráfico tenha uma legenda, indicando quem é e quem é . As legendas dentro de devem estar na mesma ordem das curvas em .
Execute o programa para ver o gráfico de e :
Passo 3
Após definir e , vamos aplicar a transformada de Fourier neles para calculá-los no domínio da frequência. Para isto, usaremos a função do MATLAB, que tem a sintaxe:
A entrada da função é um vetor contendo dados no domínio do tempo, representados por números reais. Já a saída é um vetor com números complexos: é a conversão de no domínio do tempo para o domínio da frequência. Os vetores e têm a mesma quantidade de elementos.
Logo, digite em seu programa as duas linhas de código:
![]()
Na primeira linha, calculamos a transformada de Fourier de e armazenamos o resultado em . Na segunda linha, fazemos a mesma coisa pata , cuja transformada é armazenada em .
O próximo passo é multiplicar as funções no domínio da frequência uma pela outra. Para isto, multiplicaremos o vetor por , elemento a elemento, entrando com a seguinte linha de código:
![]()
Usando o operador , multiplicamos cada elemento de pelo elemento de que está na mesma posição. O resultado dessa operação é armazenado em , que representa a convolução no domínio da frequência.
Passo 4
O vetor está no domínio da frequência e teremos o resultado da convolução ao passá-lo para o domínio do tempo. Para isto, usaremos a função do MATLAB, que tem a sintaxe:
A entrada da função é um vetor contendo dados no domínio da frequência, representados por números complexos. Já a saída é um vetor com números reais: é a conversão de no domínio da frequência para o domínio do tempo. Os vetores e têm a mesma quantidade de elementos.
Resumindo, faz o inverso de , calculando a transformada de Fourier inversa de uma função no domínio da frequência.
Portanto, inclua em seu código o comando:
![]()
Para ver o resultado da convolução, plote em função de (o domínio do tempo) com as linhas de código:
![]()
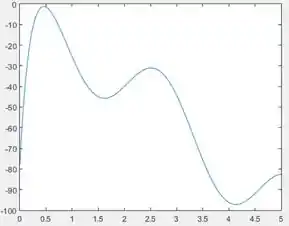
Na primeira linha, pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico do resultado da convolução em uma janela separada do primeiro gráfico. Em seguida, usamos o comando para plotar a curva da solução da convolução . Execute o programa para ver o gráfico.
Resposta