Trace um sinal senoidal com as propriedades a seguir:
- Amplitude:
- Frequência:
- Fase inicial:
- Número total de pontos de dados:
- Tempo de duração: - segundo
Verifique se o método FFT dá a mesma frequência .
Passo 1
O exercício nos dá algumas propriedades de uma onda senoidal, no domínio do tempo, e nos pede para aplicar a transformada de Fourier nela. Para isto, usaremos a função do MATLAB.
Para verificar se “o método FFT dá a mesma frequência ”, geraremos um gráfico da magnitude da onda senoidal no domínio da frequência, após a aplicação da função , e veremos as coordenadas do primeiro pico de magnitude. O pico de magnitude deve ocorrer na frequência da onda senoidal.
Passo 2
Primeiramente, vamos criar a onda senoidal no MATLAB. Em um novo script, vamos entrar as propriedades de amplitude, frequência, fase inicial e número de pontos:
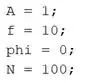
A amplitude da onda senoidal é armazenada na variável , a frequência em , a fase inicial em e o número de pontos em .
Vamos criar agora o vetor representando o intervalo de a de duração da onda. Para criar o vetor , usaremos o comando:
Neste comando, cria-se primeiro um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos de dados. Em seguida, esse vetor é multiplicado por , que é o período, em segundos, da onda senoidal.
O enunciado não nos dá o período, mas sabemos que a onda tem um intervalo de duração de a . Logo, o vetor deve começar em e terminar em . O último elemento de deve ser igual a:
Sabemos que , logo o período é igual a:
Vamos entrar essa informação no MATLAB e construir o vetor :
![]()
O vetor representa o domínio do tempo da onda senoidal.
Temos todos os dados necessários para construir a onda senoidal no domínio do tempo. No MATLAB, digite este comando para gerar a onda:
![]()
A onda senoidal é representada pelo vetor . Vamos ver a carinha dela? Digite as linhas de código abaixo no seu script para plotar o gráfico da onda senoidal no domínio do tempo:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico no domínio do tempo em uma janela diferente do gráfico no domínio da frequência (que geraremos mais pra frente, no mesmo script).
Em seguida, com o comando o gráfico da onda senoidal, no domínio do tempo, é efetivamente gerado.
Indicamos que o eixo horizontal do gráfico é o domínio do tempo por meio do comando . Temos no eixo vertical do gráfico os valores da onda senoidal, indicados por .
Ao rodarmos o programa, vemos como é a onda senoidal:

Passo 3
Vamos agora calcular a onda senoidal no domínio da frequência. Para isto, usaremos a função do MATLAB, que tem a seguinte estrutura:
A entrada da função é um vetor contendo dados no domínio do tempo, representados por numeros reais. Já a saída é um vetor com números complexos: é a conversão de no domínio do tempo para o domínio da frequência. Os vetores e têm a mesma quantidade de elementos.
Digite no seu script o comando:
![]()
Com esta linha de código, o MATLAB passará a onda senoidal, que está no domínio do tempo e é representada pelo vetor , para o domínio da frequência. A onda senoidal no domínio da frequência é representada pelo vetor .
Para verificarmos se o método FFT dá a mesma frequência de , precisamos gerar o gráfico da magnitude da onda senoidal no domínio da frequência.
Passo 4
Para construirmos o gráfico da magnitude da onda senoidal no domínio da frequência, vamos calcular a magnitude usando a função do MATLAB. Digite no MATLAB a linha de código:
![]()
Com esta linha, calculamos a magnitude de cada elemento do vetor usando a função do MATLAB. Quando a entrada da função é um número complexo, ela calcula sua magnitude.
Com esse comando, já temos o eixo vertical do gráfico, agora precisamos criar o eixo horizontal, representando o domínio da frequência. Para isto, digite os comandos:
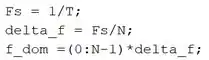
Na primeira linha, calculamos a frequência de amostragem , que é o inverso do período .
Na segunda linha, calculamos o , que é o passo do domínio da frequência: ele começa em e as frequências seguintes são obtidas pela soma de à frequência anterior. O é calculado dividindo a frequência de amostragem pelo número de pontos e é armazenado na variável .
Na terceira linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.
Primeiramente, cria-se um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos de dados. Em seguida, esse vetor é multiplicado por . Desta forma, é criado o domínio da frequência, que vai de a
Após criar o domínio da frequência, vamos usar novamente a função para gerar o gráfico da magnitude da onda senoidal no domínio da frequência:

Na primeira linha, pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico no domínio da frequência em uma janela diferente do gráfico no domínio do tempo.
Em seguida, o gráfico da magnitude de no domínio da frequência é criado com o comando Repare que, para plotar, usamos somente a primeira metade dos vetores com elementos e . Isso é indicado pela adição de à direita do nome do vetor, que diz ao MATLAB que queremos pegar do primeiro elemento ao elemento do vetor.
Usamos somente a primeira metade dos vetores e porque, no domínio da frequência, a partir de , as magnitudes começam a se repetir e não precisamos pôr elas no gráfico para encontrar o que o exercício pede.
Indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando . Temos no eixo vertical do gráfico a magnitude de , indicado por .
Passo 5
Vamos rodar o programa para ver o gráfico da magnitude da onda senoidal no domínio da frequência:

Já marquei no gráfico as coordenadas do pico de magnitude da onda senoidal no domínio da frequência. Ele ocorre em uma frequência de , muito próxima da frequência da onda senoidal, que é de . Logo, podemos dizer que o método FFT dá a mesma frequência .
Dica: caso aumentássemos o número de pontos , teríamos uma maior precisão e a frequência onde ocorre o pico de magnitude seria mais próxima de .
Resposta
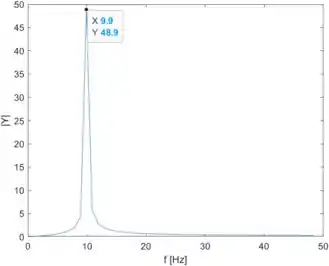
O método FFT dá a mesma frequência da onda senoidal, pois o pico de magnitude ocorre em uma frequência de , muito próxima de .