O sinal foi amostrado a uma taxa de amostras por segundo durante segundos.
- Plote o sinal
- Estime o espectro desse sinal usando . Plote a magnitude do sinal no domínio da frequência
- Estime de novo o espectro do sinal. Desta vez, adicione zeros no final do sinal de forma que seu comprimento seja igual ao dobro do comprimento original. Plote sua magnitude no domínio da frequência
- Considerando as letras [b.] e [c.], por que existem dois picos principais?
- Considerando a letra [b.], quais são as frequências (em ) dos dois picos? Por que estes picos estão nessas frequências?
- Considerando a letra [c.], quais são as frequências (em ) dos dois picos? Por que estes picos estão nessas frequências?
- Por que a frequência onde ocorre o primeiro pico das letras [e.] e [f.] é diferente? Qual letra ([e.] ou [f.]) tem a estimativa mais precisa? Como este resultado poderia ser melhorado?
Passo 1
Neste exercício, vamos calcular a transformada de Fourier de considerando duas quantidades diferentes de pontos de medição. Desta forma, vamos poder ver o impacto do númeto de pontos medidos sobre a precisão dos resultados no espectro da frequência.
Quando a questão pede para “estimar o espectro” do sinal, na prática ele pede para aplicarmos em e plotar o gráfico da magnitude do sinal no domínio da frequência.
Passo 2
A letra a do exercício pede para plotarmos . Para fazermos isso, precisamos criar um vetor representando o intervalo de tempo da medição, que vai de a segundos. Para construir esse vetor, precisamos do período da amostra, que é definido como o inverso da frequência de amostragem, isto é, . O enunciado diz que , por isso, em um script novo do MATLAB, defina o período com as linhas de código:
![]()
Com calculado, podemos criar o vetor representando o intervalo de a . Para criar o vetor , usaremos o comando:
Neste comando, cria-se primeiro um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos de dados. Em seguida, esse vetor é multiplicado por , que é o período, em segundos, do sinal.
O enunciado não nos dá o número de pontos , mas podemos calculá-lo sabendo a medição durou . Isto quer dizer que o vetor deve começar em e terminar em . Logo, o último elemento de deve ser igual a:
Como conhecemos , podemos obter a partir da equação acima. Temos que é igual a:
No seu script, entre com essa equação para calcular , construa o vetor e entre com :
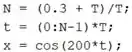
Com isso, temos tudo o que precisamos para plotar . Digite as linhas de código abaixo no seu script para plotar no domínio do tempo:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico no domínio do tempo em uma janela diferente dos gráficos no domínio da frequência (que geraremos mais pra frente, pra resolver as letras b e c, no mesmo script).
Em seguida, com o comando o gráfico de , no domínio do tempo, é efetivamente gerado.
Indicamos que o eixo horizontal do gráfico é o domínio do tempo por meio do comando . Temos no eixo vertical do gráfico os valores de , indicados por .
Ao rodarmos o programa, temos a solução da letra a:

Passo 3
A letra b pede para estimar o espectro do sinal usando , em outras palavras, para calcular o sinal no domínio da frequência. Para isto, usaremos a função do MATLAB, que tem a seguinte estrutura:
A entrada da função é um vetor contendo dados no domínio do tempo, representados por números reais. Já a saída é um vetor com números complexos: é a conversão de no domínio do tempo para o domínio da frequência. Os vetores e têm a mesma quantidade de elementos.
Digite no seu script o comando:
![]()
Com esta linha de código, o MATLAB passará o sinal , que está no domínio do tempo e é representada pelo vetor , para o domínio da frequência. O sinal no domínio da frequência é representada pelo vetor .
A letra b também pede para plotar a magnitude do sinal no domínio da frequência. Vamos calcular a magnitude usando a função do MATLAB. Digite no MATLAB a linha de código:
![]()
Com esta linha, calculamos a magnitude de cada elemento do vetor .
Já temos o eixo vertical do gráfico, agora precisamos criar o eixo horizontal, representando o domínio da frequência. Para isto, digite os comandos:
![]()
Na primeira linha, calculamos o , que é o passo do domínio da frequência: ele começa em e as frequências seguintes são obtidas pela soma de à frequência anterior. O é calculado dividindo a frequência de amostragem pelo número de pontos e é armazenado na variável .
Na segunda linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.
Primeiramente, cria-se um vetor que vai de a , com passo de (), com elementos. Em seguida, esse vetor é multiplicado por . Desta forma, é criado o domínio da frequência, que vai de a
Após criar o domínio da frequência, vamos usar novamente a função para gerar o gráfico da magnitude do sinal no domínio da frequência:

Na primeira linha, pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico no domínio da frequência em uma janela diferente do gráfico no domínio do tempo.
Em seguida, o gráfico da magnitude de no domínio da frequência é criado com o comando Indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando . Temos no eixo vertical do gráfico a magnitude de , indicado por .
Execute o programa para ter a solução da letra b:
Passo 4
A letra c pede para calcular novamente o sinal no domínio da frequência, mas adicionando zeros no final do sinal para dobrar o comprimento original. Para adicionar os zeros no sinal, vamos concatenar o vetor , que representa o sinal , com um vetor de zeros que tenha o mesmo comprimento de , adicionando ao nosso script a linha de código:
![]()
Nesta linha, criamos um vetor de zeros com a função do MATLAB, que cria uma matriz de zeros com uma linha e colunas. O comando retorna o número de elementos do vetor . Portanto, vai nos dar um vetor de zeros de mesmo tamanho de .
A concatenação dos vetores é feita colocando-os dentro de colchetes. Isto cria um vetor cuja primeira metade dos elementos é igual a e a segunda metade, um monte de zeros.
Vamos calcular o sinal novo no domínio da frequência, usando :
![]()
O novo sinal no domínio da frequência é representada pelo vetor .
A letra c também pede para plotar a magnitude do sinal novo no domínio da frequência. Novamente, vamos usar a função para calcular a magnitude :
![]()
O resultado é armazenado no vetor , que será o eixo vertical do gráfico.
Precisamos recriar o eixo horizontal representando o domínio da frequência, pois a adição dos zeros alterou o número de pontos da medição. O novo número de pontos é igual à quantidade de elementos de , dada pela função :
![]()
Com o novo número de pontos, precisamos recalcular o passo do domínio da frequência e atualizar o domínio da frequência, com os comandos:
![]()
O novo passo é e o novo domínio é o vetor .
vamos usar novamente a função para plotar a magnitude do novo sinal no domínio da frequência:

Na primeira linha, pedimos ao MATLAB para gerar uma terceira figura com o comando . Em seguida, o gráfico da magnitude de no domínio da frequência é criado com o comando
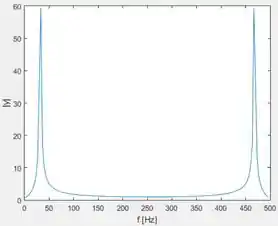
Execute o programa para ter a solução da letra c:
Passo 5
A letra d pergunta por que os dois gráficos no domínio da frequência tem dois picos principais. Isso ocorre porque a função do MATLAB é válida para um intervalo no domínio da frequência que vai de . A partir de , os resultados da se repetem, de forma espelhada. Na prática, poderíamos só plotar a primeira metade do gráfico.
Passo 6
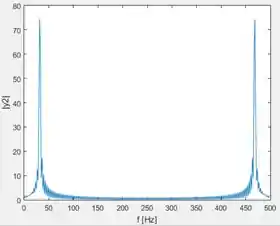
A letra e pergunta em quais frequências ocorrem os dois picos no gráfico gerado na letra b e por que os picos ocorrem nessas frequências.
No print abaixo temos o gráfico da letra com as coordenadas dos dois picos:
O primeiro pico ocorre a uma frequência de e o segundo, a (que é exatamente igual a , reforçando a resposta da letra d).
O gráfico acima é o sinal no domínio da frequência. A frequência de é igual a:
Os picos de sinais periódicos no domínio da frequência ocorrem na frequência máxima do sinal quando a frequência de amostragem () é pelo menos o dobro da frequência da onda (). Este é o teorema de amostragem de Nyquist. No gráfico acima, o primeiro pico ocorre a , uma frequência muito próxima de . Isso ocorre porque o teorema de amostragem de Nyquist foi respeitado.
Passo 7
A letra f pergunta em quais frequências ocorrem os dois picos no gráfico gerado na letra c e por que os picos ocorrem nessas frequências.
No print abaixo temos o gráfico da letra com as coordenadas dos dois picos:
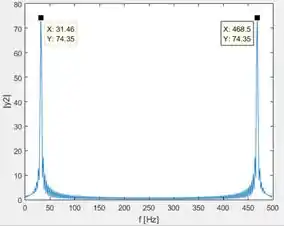
O primeiro pico ocorre a uma frequência de e o segundo, a (que é exatamente igual a ).
O gráfico acima é o sinal com o dobro de pontos no domínio da frequência. Como vimos no passo anterior, a frequência de é igual a . Como neste caso o teorema de amostragem de Nyquist também foi respeitado, temos que o primeiro pico ocorre a uma frequência muito próxima de , até mais próxima do que o caso original.
Passo 8
A letra g pergunta por que a frequência onde ocorre o primeiro pico das letras e e g é diferente, qual das duas tem a estimativa mais precisa e como podemos melhorar o resultado.
A frequência onde ocorrem os picos é diferente porque o número de pontos da amostra é diferente (). A letra g, que tem o espectro de com o dobro de pontos, é a estimativa mais precisa, exatamente por ter mais pontos. Isso é evidenciado pelo fato de o primeiro pico da letra g ocorre em uma frequência () mais próxima à frequência de (). Para melhorar o resultado, podemos diminuir o período de amostragem, ou seja, podemos aumentar a frequência de amostragem . Isso faz com que tenhamos mais pontos na amostra, deixando o resultado mais preciso.
Resposta


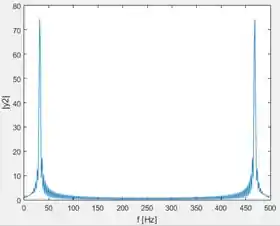
- A função do MATLAB é válida para um intervalo no domínio da frequência que vai de . A partir de , os resultados da se repetem, de forma espelhada.
- O primeiro pico ocorre a uma frequência de e o segundo, a . Segundo o teorema de amostragem de Nyquist, os picos de sinais periódicos no domínio da frequência ocorrem na frequência máxima do sinal no domínio do tempo quando a frequência de amostragem é pelo menos o dobro da frequência da onda.
- O primeiro pico ocorre a uma frequência de e o segundo, a . Os picos ocorrem nessa frequência por causa do teorema de amostragem de Nyquist.
- A frequência onde ocorrem os picos é diferente porque o número de pontos da amostra é diferente. A letra g, que tem o espectro de com o dobro de pontos, é a estimativa mais precisa. Isso é evidenciado pelo fato de o primeiro pico da letra g ocorre em uma frequência () mais próxima à frequência de (). Para melhorar o resultado, podemos diminuir o período de amostragem, ou seja, podemos aumentar a frequência de amostragem . Isso faz com que tenhamos mais pontos de medição, deixando o resultado mais preciso.