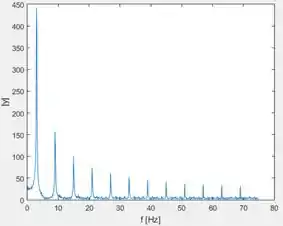
O sinal de uma onda quadrada com frequência de tem pontos e foi amostrado a uma taxa de amostras por segundo. Plote a onda quadrada no domínio do tempo e use o método da transformada de Fourier para plotar a magnitude do sinal no domínio da freqüência.

Primeiramente, vamos entrar no MATLAB as informações fornecidas pelo enunciado: a frequência da onda quadrada, a taxa de amostragem e o número de pontos :

Em seguida, podemos calcular o período de amostragem (que é o inverso de ) e criar um vetor representando o domínio do tempo:

Para construir o vetor , cria-se primeiro um vetor que vai de a , com passo de (). Este vetor tem elementos, correspondendo aos pontos do sinal. Em seguida, esse vetor é multiplicado por .

Tendo definido o domínio do tempo, podemos construir a onda quadrada, por meio do comando , que tem a sintaxe:

Ela retorna uma onda quadrada de amplitude com frequência para um vetor representando o tempo. A onda quadrada é armazenada no vetor .

Em seu programa, adicione o comando:

Este comando gerará a onda quadrada de frequência com vetor que criamos acima. Note que a frequência foi convertida de para , fazendo .

Para plotar a onda quadrada no domínio do tempo, entre com as linhas de código:

Na primeira linha, pedimos ao MATLAB para gerar uma figura com o comando , para termos o gráfico no domínio do tempo em uma janela diferente do gráfico no domínio da frequência. Em seguida, com o comando o gráfico da onda quadrada no domínio do tempo é efetivamente gerado.

Indicamos que o eixo horizontal do gráfico é o domínio do tempo por meio do comando . Temos no eixo vertical do gráfico os valores de , indicados por .

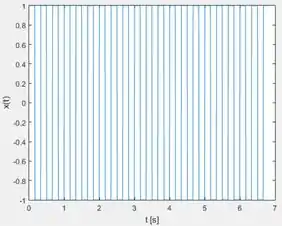
Rodando o programa, temos o gráfico da onda quadrada:

Vamos aplicar o método da transformada de Fourier para plotar a magnitude do sinal no domínio da frequência. Para isto, usaremos a função do MATLAB, que tem a seguinte estrutura:

A entrada da função é um vetor contendo dados no domínio do tempo, representados por números reais. Já a saída é um vetor com números complexos: é a conversão de no domínio do tempo para o domínio da frequência. Os vetores e têm a mesma quantidade de elementos.

Digite no seu script o comando:

Com esta linha de código, o MATLAB passará o sinal da onda quadrada no domínio do tempo, representada pelo vetor , para o domínio da frequência. O sinal no domínio da frequência é representada pelo vetor .

Após aplicar a transformada de Fourier, vamos calcular a magnitude do sinal no domínio da frequência. Para isto, usaremos a função do MATLAB. Digite no MATLAB a linha de código:

Com esta linha, calculamos a magnitude de cada elemento do vetor .

Já temos o eixo vertical do gráfico da onda quadrada no domínio da frequência, agora precisamos criar o eixo horizontal, representando o domínio da frequência. Para isto, digite os comandos:

Na primeira linha, calculamos o , que é o passo do domínio da frequência: ele começa em e as frequências seguintes são obtidas pela soma de à frequência anterior. O é calculado dividindo a frequência de amostragem pelo número de pontos e é armazenado na variável .

Na segunda linha, geramos o domínio da frequência, representado pelo vetor . A lógica da sua criação é igualzinha à lógica que usamos para criar o vetor , do domínio do tempo.

Primeiramente, cria-se um vetor que vai de a , com passo de (), com elementos. Em seguida, esse vetor é multiplicado por . Desta forma, é criado o domínio da frequência, que vai de a

Após criar o domínio da frequência, vamos usar novamente a função para gerar o gráfico da magnitude do sinal no domínio da frequência:

Na primeira linha, pedimos ao MATLAB para gerar uma segunda figura com o comando , para termos o gráfico no domínio da frequência em uma janela diferente do gráfico no domínio do tempo.

Em seguida, o gráfico da magnitude de no domínio da frequência é criado com o comando Repare que, para plotar, usamos somente a primeira metade dos vetores com elementos e . Isso é indicado pela adição de à direita do nome do vetor, que diz ao MATLAB que queremos pegar do primeiro elemento ao elemento do vetor. Fazemos isso pois, no domínio da frequência, a partir de , as magnitudes começam a se repetir e seria redundante plotá-las.

Indicamos que o eixo horizontal do gráfico é o domínio da frequência por meio do comando . Temos no eixo vertical do gráfico a magnitude de , indicado por .

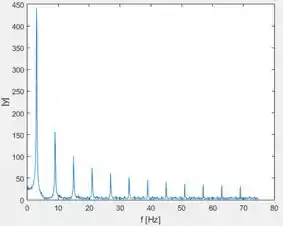
Execute o programa e você terá a magnitude da onda quadrada no domínio da frequência: