O circuito RLC abaixo pode ser usado como um filtro de banda estreita. Se a tensão de entrada consiste na soma de tensões de variação sinusoidal com diferentes frequências, o filtro de banda estreita permitirá passar somente tensões cujas frequências estão dentro de uma faixa estreita. Esses filtros são usados em circuitos de sintonia, como os usados em rádios AM, para permitir a recepção apenas do sinal portador da estação de rádio desejada.

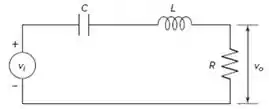
O circuito RLC tem a seguinte equação diferencial:

Onde é a tensão de saída.

Use o método da transformada de Laplace para encontrar a resposta ao degrau unitário de para condições iniciais nulas, onde e . Para modelar um filtro de banda larga, use . Já para modelar um filtro de banda estreita, use . Compare a resposta ao degrau dos dois casos.

Comece entrando com a equação diferencial no MATLAB, termo a termo. Em um script novo, digite as linhas de código:

Na primeira linha, criamos as variáveis simbólicas , , e , indicando que é em função de .

Na segunda linha, calculamos a derivada usando a função do MATLAB. Como estamos trabalhando com variáveis simbólicas, apenas representa a derivada de em relação a e é armazenado em .

Na terceira linha, calculamos a derivada , pedindo ao MATLAB para calcular a derivada de em relação a ().

Na quarta linha, criamos um degrau unitário em função de usando a função , representando a tensão de entrada do circuito.

Na quinta linha, definimos a primeira derivada do degrau unitário usando . A derivada é armazenada em .

Tendo definido os termos da equação, vamos criá-la e armazená-la na variável :

Repare que joguei todos os termos da equação da para a esquerda, para fazer com que ela seja igual a .

Com a equação diferencial no MATLAB, podemos usar a função para calcular a transformada de Laplace dela. Lembrando que tem como estrutura:

Ela retorna a transformada de Laplace da função , armazenando-a na variável .

Acrescente em seu programa o comando abaixo para calcular a transformada de Laplace de :

O resultado é armazenado em . Vamos ver como ele ficou? Rode o programa que fizemos até agora e imprima no Command Window:

Ficou uma expressão bem comprida, tive que deixar a letra minúscula para caber aqui. Mas podemos dar uma enxugada nessa expressão: note que aparecem uns termos em , e eles têm exatamente a mesma estrutura da função . Essa expressão representa a transformada de Laplace de e pode ser substituída por . No caso, chamaremos só de .

Digite os comandos abaixo para fazer a substituição:

Primeiramente, devemos criar mais duas variáveis simbólicas: e . Em seguida, usamos a função para pedir ao MATLAB que substitua em a expressão por . O resultado da substituição é armazenado em , atualizando a expressão anterior. Após a susbtituição, fica assim:

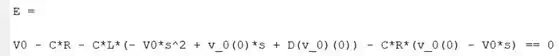
Já deu uma boa enxuagada. Agora vamos substituir as condições iniciais em . O enunciado disse que elas são nulas, logo, . Na expressão acima, é fácil de identificar quem é . Já é representado por , um pouco mais sutil.

Para fazer as substituições, adicione ao seu programa a linha de código:

Com este comando, substituímos em e por e armazenamos a nova expressão em , no lugar da antiga. Note que usei aspas simples em , para indicar que os parênteses pertencem a uma expressão só. Se você tentar rodar o programa sem elas, o MATLAB acusará erro de sintaxe.

Agora está assim:

Agora podemos encontrar . Para isto, precisamos encontrar para daí aplicar nele , para termos a inversa da tranformada de Laplace. Em , a variável representa e podemos usar a função do MATLAB para encontrá-la. Adicione em seu código:

Com este comando, a função resolve a equação para a variável e armazena a solução em , atualizando seu valor. Na prática, isolamos na equação e passa a representar a expressão algébrica de . Rodando o programa, temos que é igual a:

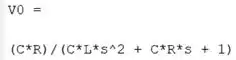
Para encontrarmos , devemos aplicar a inversa da transformada de Laplace em , isto é, usar a função do MATLAB em . A função tem a estrutura:

Ela retorna a inversa da transformada de Laplace de , armazenando-a na variável .

Logo, em seu código, entre o comando:

Com este comando, o MATLAB calcula a inversa da transformada de Laplace de e armazena o resultado em , atualizando seu valor. é a solução da equação diferencial, representadno a resposta do sistema ao degrau unitário. Rodando o programa, temos que é igual a:

A expressão acima ficou grandinha, mas ela vai encolher quando substituirmos , e pelos valores fornecidos no enunciado.

Vamos comparar as respostas ao degrau de um filtro de banda larga, com , e de um filtro de banda estreita, com . O primeiro passo é substituir em e por e , usando o comando :

Com este comando, foi atualizado com valores numéricos de e .

Em seguida, vamos substituir por , para ver a resposta ao degrau do filtro de banda larga:

Armazenamos em a expressão de com . Vamos ver como ela ficou?

Podemos transformar as frações e as exponenciações em números decimais, usando o comando do MATLAB. Este comando avalia cada elemento de uma expressão simbólica e identifica as frações ou as exponenciações com números reais, e as transforma em números “quebrados”. Por isso, acrescente no seu código o comando:

Este comando aplica a função em e armazena o resultado em , substituindo a expressão anterior. Ele vai nos dar os coeficientes de com algarismos significativos. Ao rodar programa, podemos ver com seus coeficientes transformados em números decimais:

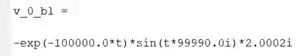
Repare que tem números complexos, identificados por multiplicarem .

Vamos agora ver como é em um filtro de banda estreita, isto é, vamos substituir por :

Armazenamos em a expressão de com . Rode o programa e imprima-a no Command Window para ver

Bem mais simpática que , não?