A equação diferencial que modela um certo sistema de controle de posição de uma ferramenta de corte de metal é

Onde a posição real da ferramenta é , a posição desejada é , e , e são constantes chamadas “ganhos”. Use o método da transformada de Laplace para encontrar a resposta ao degrau unitário (isto é, é uma função degrau unitário). Use condições iniciais nulas. Compare a resposta para três casos:

Comece entrando com a equação diferencial no MATLAB, termo a termo. Em um script novo, digite as linhas de código:

Na primeira linha, são criadas as variáveis simbólicas , , e , sendo indicado que é em função de .

Na segunda linha, calculamos a derivada usando a função do MATLAB. Como estamos trabalhando com variáveis simbólicas, apenas representa a derivada de em relação a e é armazenado em .

Na terceira linha, calculamos a derivada , pedindo ao MATLAB para calcular a derivada de em relação a (). A segunda derivada de é registrada em .

Na quarta linha, calculamos a derivada , pedindo ao MATLAB para calcular a derivada de em relação a (). A terceira derivada de é registrada em .

Na quinta linha, criamos um degrau unitário em função de usando a função , representando a posição desejada da ferramenta.

Na sexta linha, definimos a primeira derivada do degrau unitário usando . A derivada é armazenada em .

Finalmenten na sétima linha, é definida a segunda derivada , aplicando em e derivando-o em relação a (). é registrada em .

Tendo definido os termos da equação, vamos criá-la e armazená-la na variável , jogando todos os termos para a esquerda da igualdade e fazendo com que :

Note que usei o recurso dos três pontos (...) para “quebrar” a linha de código, de forma que conseguimos ver inteira sem ter que usar uma barra de rolagem.

Tendo entrado a equação diferencial no MATLAB, vamos usar a função para calcular a transformada de Laplace dela. Lembrando que tem a sintaxe:

Ela retorna a transformada de Laplace da função , armazenando-a na variável .

Acrescente em seu programa o comando abaixo para calcular a transformada de Laplace de :

A transformada de é armazenada em . Para ver como ficou, execute o programa que fizemos até agora e imprima no Command Window:

ficou tão grande que quebrei ele em três prints, mas já vamos dar uma boa enxugada nele. Note que aparecem uns termos em , e eles têm exatamente a mesma estrutura da função . Essa expressão representa a transformada de Laplace de e pode ser substituída por . No caso, chamaremos só de .

Para fazer a substituição, implemente as linhas de código:

Primeiramente, criamos mais duas variáveis simbólicas: e . Em seguida, usamos a função para pedir ao MATLAB que substitua em a expressão por . O resultado da substituição é armazenado em , atualizando a expressão anterior. Após a susbtituição, fica assim:

Novamente, tive que quebrar em mais de um print, porque ainda tá enorme. Vamos fazer mais uma substituiçãozinha: o enunciado disse que as condições iniciais são nulas, isto é, . Na expressão acima, identificamos de cara quem é x. Já e não são tão evidentes: elas são representadas por e , respectivamente.

Para fazer as substituições das condições iniciais, adicione ao seu programa a linha de código:

Com este comando, substituímos em , e por e armazenamos a nova expressão em , no lugar da antiga. Note as aspas simples em e , elas indicam que os múltiplos parênteses pertencem a uma expressão só, isto é, compõem uma variável simbólica. Se você tentar rodar o programa sem elas, o MATLAB acusará erro de sintaxe.

Vamos ver a nova cara de :

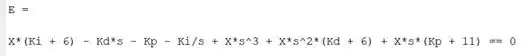
Ficou bem mais bonitinho =)

Com o mais enxuto, podemos encontrar . Para isto, precisamos encontrar para daí aplicar nele , para termos a inversa da tranformada de Laplace. Em , a variável representa e podemos usar a função do MATLAB para encontrá-la. Adicione em seu código:

Com este comando, a função resolve a equação para a variável e armazena a solução em , atualizando seu valor. Na prática, isolamos na equação e passa a representar a expressão algébrica de . Rodando o programa, temos que é igual a:

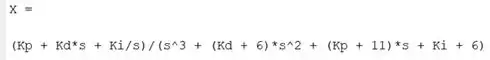
Para encontrarmos , devemos aplicar a inversa da transformada de Laplace em , isto é, usar a função do MATLAB em . A função tem a estrutura:

Ela retorna a inversa da transformada de Laplace de , armazenando-a na variável .

Logo, em seu código, adicione o comando:

Com este comando, o MATLAB calcula a inversa da transformada de Laplace de e armazena o resultado em , atualizando seu valor. é a solução da equação diferencial, representando a resposta do sistema ao degrau unitário.

Se você rodar o programa para ver , você vai ver que ele ficou uma expressão bem longa, com algumas comandos esquisitos (tipo ). Vamos fazer a substituição dos ganhos , e para plotar curvas de , facilitando a comparação das respostas ao degrau.

As opções de substituição são:

Para implementá-las no nosso programa, usaremos a função e substituiremos as variáveis , e de pelos ganhos apresentados acima:

Na primeira linha, substituímos em as variáveis , e pelos ganhos da letra a e armazenamos o resultado em .

Nas linhas seguintes, fazemos a mesma coisa para os ganhos das letras e , registrando a substituição nas variáveis e , respectivamente.

Para plotar as curvas de , e , criamos um vetor , indo de a . A ideia é substituir a variável simbólica das expressões de , e por cada elemento de e calcular o valor numérico de , e . Para isto, usaremos o comando para fazer a substituição de pelo vetor e usaremos a função para converter o resultado de simbólico para valores numéricos:

Por exemplo, na segunda linha acima, a variável simbólica é substituída por cada elemento do vetor em . O resultado dessa substituição é convertido de simbólico para numérico usando . O resultado da conversão é o vetor , que contém os valores de para cada elemento de tempo. O mesmo é feito para e .

Para gerar as curvas das respostas ao degrau, digite os dois comandos:

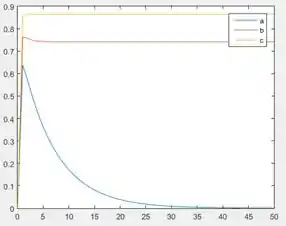
A função gerará o gráfico com as curvas de em relação a , em relação a e em relação a .

O comando cria a legenda do gráfico, indicando que o primeiro par de vetores de representa a curva da resposta ao degrau com os ganhos de a, o segundo par, com os ganhos de b e o último par, com os ganhos de c.

Ao executar o programa, você terá as curvas de para cada uma das três alternativas de ganhos.