A equação diferencial que modela o torque de um motor exigido para um certo sistema de controle de velocidade é
Onde é a velocidade desejada e é uma constante chamada “ganho”.
Use o método da transformada de Laplace para encontrar a resposta ao degrau unitário (isto é, é uma função degrau unitário). Use condições iniciais nulas.
Passo 1
O exercício pede para encontrarmos a resposta do torque a igual a um degrau unitário, usando a transformada de Laplace. Em outras palavras, vamos encontrar a solução da equação diferencial de segunda ordem dada pelo enunciado. Primeiramente, aplicaremos a função do MATLAB na equação diferencial para encontrarmos a transformada de .
Como o enunciado não especificou nada, consideraremos que a variável independente das transformadas de Laplace é , que é o padrão do MATLAB. Logo, a transformada de Laplace de será .
Após encontrarmos , vamos aplicar para encontrar a inversa da transformada, isto é, , que é a solução da equação diferencial.
Passo 2
Vamos começar entrando com a equação diferencial no MATLAB, termo a termo. Em um script novo, digite as linhas de código:

Na primeira linha, criamos as variáveis simbólicas e , indicando que é em função de .
Na segunda linha, calculamos a derivada usando a função do MATLAB. Como estamos trabalhando com variáveis simbólicas, apenas representa a derivada de em relação a e é armazenado em .
Na terceira linha, calculamos a derivada , pedindo ao MATLAB para calcular a derivada de em função de ().
Na quarta linha, criamos um degrau unitário em função de usando a função , representando a velocidade desejada do motor.
Na quinta linha, definimos a primeira derivada do degrau unitário usando . A derivada é armazenada em .
Tendo definido os termos da equação, vamos criá-la e armazená-la na variável :
![]()
Note que joguei todos os termos da equação diferencial para a esquerda, e que fiz tudo igual a .
Passo 3
Com a equação diferencial no MATLAB, podemos usar a função para calcular a transformada de Laplace dela. Lembrando que tem como estrutura:
Ela retorna a transformada de Laplace da função , armazenando-a na variável .
Acrescente em seu programa o comando abaixo para calcular a transformada de Laplace de :
![]()
O resultado é armazenado em . Vamos ver como ele ficou? Rode o programa que fizemos até agora e imprima no Command Window:
![]()
Ficou um expressão bem comprida, tá até difícil de ler.
Vamos resolver isso fazendo umas substituições. Perceba que o MATLAB usa em alguns elementos de , que tem exatamente a mesma estrutura da função . Essa expressão representa a transformada de Laplace de e pode ser substituída por . No caso, chamaremos só de .
Adicione os comandos abaixo em seu programa para fazer a substituição:
![]()
Primeiramente, devemos criar mais duas variáveis simbolicas: e . Em seguida, usamos a função para pedir ao MATLAB que substitua em a expressão por . O resultado da substituição é armazenado em , substituindo a expressão anterior. Após a susbtituição, fica assim:
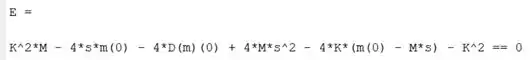
Melhorou bastante, né? Agora vamos substituir as condições iniciais em . O enunciado disse que elas são nulas, logo, . Na expressão acima, é fácil de identificar quem é . Já é representado por .
Para fazer as substituições, adicione ao seu programa a linha de código:
![]()
Com este comando, substituímos em e por e armazenamos a nova expressão em , no lugar da antiga. Note que usei aspas simples em . Elas servem para indicar que é uma expressão só. Se você tentar rodar o programa sem elas, o MATLAB acusará erro de sintaxe.
Vamos ver a nova cara de :
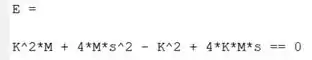
Passo 4
Agora podemos encontrar . Para isto, precisamos encontrar para daí aplicar nele , para termos a inversa da tranformada de Laplace. Em , a variável representa e podemos usar a função do MATLAB para encontrá-la. Adicione em seu código:
![]()
Com este comando, a função resolve a equação para a variável e armazena a solução em , atualizando seu valor. Na prática, isolamos na equação com este comando e passa a representar a expressão algébrica de . Rodando o programa, temos que é igual a:

Passo 5
Para encontrarmos , devemos aplicar a inversa da transformada de Laplace em , isto é, usar a função do MATLAB em . A função tem a estrutura:
Ela retorna a inversa da transformada de Laplace de , armazenando-a na variável .
Para encontrar , entre o comando:
![]()
Com este comando, o MATLAB calcula a inversa da transformada de Laplace de e armazena o resultado em , atualizando seu valor. é a solução da equação diferencial, representadno a resposta do sistema ao degrau unitário. Rodando o programa, temos que é igual a:

Resposta
A resposta ao degrau unitário é: