Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Identificando as Cônicas

Ver Todos os Exercícios

Teoria

Cônicas

Pra finalizar o assunto, agora vamos ver como reconhecer algumas quádricas, especialmente as cônicas do R ² . Fazemos isso olhando a cara da equação, podendo ela estar simplificada ou até bem feia.

Elipse

Um exemplo de elipse é a curva definida pela equação:

x 2 + 4 y 2 = 4

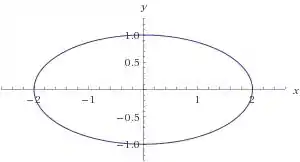
A equação equivale também à:

x 2 4 + y 2 1 = 1

Assim, a equação geral de uma elipse é:

x 2 a 2 + y 2 b 2 = 1

Onde a e b são os semieixos.

Cuidado!!! Pra elipse e pras cônicas seguintes quando a gente falar de equação geral quer dizer somente que todas as cônicas desse tipo tem a equação simplificada desse jeito. Se aparecer termos mistos e lineares nós vamos simplificar como vimos agora a pouco e ver no que dá.

Hipérbole

Um exemplo de hipérbole é a curva definida pela equação:

x 2 - y 2 = 1

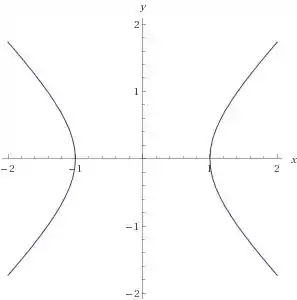
E a equação geral:

x 2 a 2 - y 2 b 2 = 1

Se ligue que se aparecer:

y 2 b 2 - x 2 a 2 = 1

Também é uma hipérbole, só tocamos as coordenadas.

Parábola

Um exemplo de parábola é a conhecida curva:

y = x ²

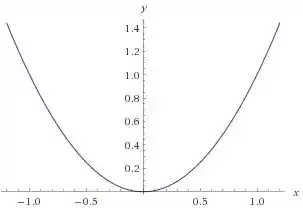
E a equação geral:

y = a x ²

De novo, vale também:

x = a y ²

O que vamos ter que fazer geralmente é simplificar as equações que os derem e ver de qual tipo é a equação em que chegamos.

Cuidado com as degenerações

Tem uma coisa muito perigosa que a galera geralmente aprende. Eu vou mostrar aqui o que é mas ATENÇÃO, esse método não é muito bom pois não dá pra verificar as degenerações.

Se a equação da cônica é:

A x 2 + B x y + C y 2 + D x + E y + F = 0

E:

Δ = B 2 - 4 A C

Tipo o da Fórmula de Bháskara, temos que:

Δ < 0 ⇒ Elipse

Δ = 0 ⇒ Parábola

Δ > 0 ⇒ Hipérbole

Isso em geral funciona, MAS NEM SEMPRE!! Porquê??

Veja por exemplo a quádrica:

x 2 2 - y 2 2 - 2 2 y - 2 x = 3

Temos:

Δ = 1

Logo esperamos que seja uma hipérbole, mas ela é na verdade isso aqui:

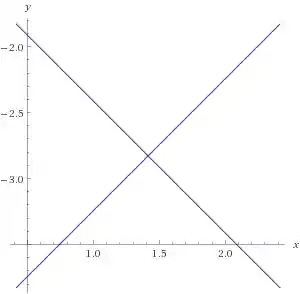
Um par de retas!! Vamos simplificar a equação e ver porquê. Completando quadrados:

x 2 2 - y 2 2 - 2 2 y - 2 x - 3 = 0

x 2 2 - 2 x + 1 - y 2 2 + 2 2 y + 4 - 3 = - 4 + 1

x 2 - 1 2 - y 2 + 2 2 = 0

1 2 x - 2 2 - 1 2 y + 2 2 2 = 0

Fazendo:

x 2 = x 1 - 2

y 2 = y + 2 2

Chegamos em:

x 2 - y 2 = 0

Ou:

x - y x + y = 0

x - y = 0     o u   x + y = 0

Ou seja, um par de retas. Essas degenerações podemos ver simplificando as equações, mas não com o método do Δ . Esse método não é inútil, serve para diferenciar entre os 3 tipos de cônica. Por exemplo, se o Δ de uma equação for 0 , ela não pode descrever uma hipérbole ou uma elipse, só uma parábola ou uma degeneração desta.

Mais uma vez pra fixar, cuidado com as degenerações.

Agora você pode estar se perguntando, cadê as quádricas do R ³ .

Quando passamos para o R 3 as coisas ficam mais complicadas, não existindo nem um consenso sobre como chamar cada coisa. Além disso, esse caso não cai nas provas. Então não se preocupe.

Bora que vamos!

Cuidado com as degenerações

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Determine se a curva determinada por:

4 x 2 + 9 y 2 = 1

É uma hipérbole, parábola ou elipse.

Passo 1

Para determinarmos qual tipo é, precisamos ver com qual tipo de equação a nossa se adequa:

x 2 a 2 + y 2 b 2 = 1

x 2 a 2 - y 2 b 2 = 1

y = a x ²

Vamos lá

Passo 2

Só mudando as coisas um pouquinho, vemos que:

4 x 2 + 9 y 2 = 1

Equivale à:

x 2 1 2 2 + y 2 1 3 2 = 1

Logo fazendo a = 1 2 e b = 1 3   vemos que trata-se de uma equação do tipo:

x 2 a 2 + y 2 b 2 = 1

Logo trata-se de uma elipse

Resposta

Elipse

Exercício Resolvido #2

Elaboração própria

Determine se a curva determinada por:

x 2 - 4 y 2 = - 4

É uma hipérbole, parábola ou elipse.

Passo 1

Para determinarmos qual tipo é, precisamos ver com qual tipo de equação a nossa se adequa:

x 2 a 2 + y 2 b 2 = 1

x 2 a 2 - y 2 b 2 = 1

y = a x ²

Vamos lá

Passo 2

Dividindo a equação:

x 2 - 4 y 2 = - 4

Por - 4 , chegamos em:

y 2 - x 2 2 2 = 1

E lembrando que se trata somente de uma mudança de coordenadas, ela equivale à:

x 2 a 2 - y 2 b 2 = 1

Logo se trata de uma hipérbole.

Resposta

Hipérbole.

Exercício Resolvido #3

P3 MAT2458 USP. Ano: 2008. Questão 1

Passo 1

Aqui precisamos achar a restrição sobre as constantes D e F para que a equação descreva uma hipérbole. Como:

Δ = - 4.1 . - 1 = 4 > 0

Precisamos evitar simplesmente as degenerações. Pra isso vamos simplificar a equação e ver no que dá.

Passo 2

Completando os quadrados:

x 2 - y 2 + 2 D x + F = 0

x 2 + 2 D x + D 2 - y 2 + F = D ²

x + D 2 - y 2 = D 2 - F

Fazendo:

x 2 = x 1 + D

x 2 - y 2 = D 2 - F

Agora pense comigo, se D 2 - f > 0   dá pra gente dividir a equação por isso echegar na eq. geral da hipérbole, o mesmo se D 2 - f < 0 . Logo basta que:

D 2 - f ≠ 0

Para que seja uma hipérbole

Resposta

d     D 2 - f ≠ 0

Exercício Resolvido #4

P3 MAT2458 USP. Ano: 2008. Questão 16

Passo 1

Aqui precisamos ver o que a quádrica representa. Como:

Δ = - 4.1 . - 1 = 4 > 0

Se não for uma degeneração será uma hipérbole. Mas resta checarmos por elas.

Passo 2

Vamos fazer de um jeito diferente agora: fatorar.

y 2 - x 2 - y - x = 0

y - x y + x - y - x = 0

y - x y + x - 1 = 0

Logo:

y - x = 0 ou y + x - 1 = 0

Tratam-se então do par de retas concorrentes:

r 1 :       y = x

r 2 :       y = - x + 1

Resposta

d   Um par de retas concorrentes

Exercício Resolvido #5

P3 MAT2458 - USP. Ano: 2008. Questão 18

Seja C   ∈ R . Uma condição necessária e suficiente para que a cônica de equação x 2 + y 2 + 2 C x y - 2 2 x + 1 = 0 seja uma parábola é:

  1. C = 0 ;
  2. C = 1 ;
  3. C = 1   o u   C = - 1 ;
  4. C = - 1 ;
  5. C ≠ 0 .

Passo 1

Aqui precisamos achar a restrição sobre a constante C para que a equação descreva uma parábola. Para que seja uma parábola, temos que Δ = 0 :

4 C 2 - 4 = 0

C = ± 1

Passo 2

Vamos checar para C = 1 se a equação é uma degeneração:

x 2 + y 2 + 2 x y - 2 2 x + 1 = 0

Um jeito de verificarmos se existe uma degeneração é tentarmos resolver a equação de 2º grau para y . Com Bháskara mesmo!! Se o Δ for um quadrado perfeito vamos achar uma degeneração:

Δ = 4 x 2 - 4.1 . ( x 2 - 2 2 x + 1 )

Δ =   8 2 x - 4

Como não é o caso, não se trata de uma degeneração e sim de uma parábola!

Passo 3

Vamos checar para C = - 1 se a equação é uma degeneração:

x 2 + y 2 - 2 x y - 2 2 x + 1 = 0

Seguimos o mesmo procedimento:

Δ = 4 x 2 - 4.1 . ( x 2 - 2 2 x + 1 )

Δ =   8 2 x - 4

Mesma situação, se trata de uma parábola!!

Resposta

c   C = 1 ou C = - 1

Exercício Resolvido #6

P3-MAT2458-USP. Ano: 2008. Questão 20

Seja F ∈ R . A cônica de equação 9 x 2 + y 2 - 6 x y = 10 F 2 é :

  1. Um par de retas paralelas se e somente se F < 0 ;
  2. Um par de retas concorrentes se e somente se F > 0 ;
  3. Um par de retas paralelas se e somente se F ≠ 0 ;
  4. Um par de retas paralelas se e somente se F > 0 ;
  5. Um par de retas concorrentes se e somente se F ≠ 0 .

Passo 1

Aqui precisamos considerar a influência de F na cônica. Primeiramente, vamos simplificar a equação.

Passo 2

Temos:

q C a n = 9 - 3 - 3 1

Calculamos os autovalores:

det ⁡ q C a n - λ I = 9 - λ - 3 - 3 1 - λ = 0

9 - λ 1 - λ - 9 = 0

λ 2 - 10 λ = 0

λ 1 = 0 λ 2 = 10

Logo a equação simplificada é:

10 y 2 = 10 F ²

y 2 = F ²

Passo 3

E agora?

Bem, se F = 0 :

y 2 = 0 ⇒ y = 0

Ou seja, temos uma única reta.

Agora, se F ≠ 0 , temos:

y = ± F 2

Obs: Não tiramos o F da raiz por não sabermos se é positivo ou negativo.

De qualquer forma, teremos uma par de retas paralelas!!

Resposta

c   Um par de retas paralelas se e somente se F ≠ 0

Exercício Resolvido #7

P3 MAT2458 USP. Ano: 2009. Questão 6

Passo 1

Aqui precisamos considerar a influência de a na cônica. Primeiramente, vamos simplificar a equação.

Passo 2

Temos:

q C a n = a - 1 - 1 a

Calculamos os autovalores:

det ⁡ q C a n - λ I = a - λ - 1 - 1 a - λ = 0

a - λ a - λ - 1 = 0

λ 2 - 2 a λ + a 2 - 1 = 0

λ 1 = a + 1 λ 2 = a - 1

Logo a equação simplificada é:

a + 1 x 2 + a - 1 y 2 = 1

Passo 3

E agora?

Bem, se 0 < a < 1 , a equação fica:

x 2 k 1 2 - y 2 k 2 2 = 1

Então se trata de uma hipérbole, logo (I) é verdadeiro.

Se a = 1 :

2 x 2 = 1

x = ± 2 2

Logo temos um par de retas paralelas: (II) é verdadeiro.

Por fim, se a > 1 :

x 2 k 1 2 + y 2 k 2 2 = 1

Então temos uma elipse. (III) é verdadeiro

Resposta

b   Todas as afirmações são verdadeiras.

Exercício Resolvido #8

P3-MAT2458-USP. Ano: 2012. Questão 6

Passo 1

Aqui precisamos considerar a influência de b na cônica. Primeiramente, vamos simplificar a equação.

Passo 2

Temos:

q C a n = 3 4 4 3

Calculamos os autovalores:

det ⁡ q C a n - λ I = 3 - λ 4 4 3 - λ = 0

3 - λ 2 - 16 = 0

λ 2 - 6 λ - 7 = 0

λ 1 = 7 λ 2 = - 1

Logo a equação simplificada é:

7 x 2 - y 2 = b

Passo 3

E agora?

Se b ≠ 0 , podemos dividir a equação por este e obter a eq. de uma hipérbole

Logo, se b > 0   e b < 0 , temos uma hipérbole. (I) falso e (II) verdadeiro.

Agora, se b = 0 :

y 2 = 7 x ²

y = ± 7 x

Logo temos um par de retas concorrentes. (III) é verdadeiro.

Resposta

a   Apenas as afirmações (II) e (III) verdadeiras

Exercício Resolvido #9

P3 MAT2458 USP. Ano: 2011. Questão 6

Passo 1

Apesar de não estarmos reconhecendo cônicas normalmente aqui, estamos procurando por um valor de k correspondente à degeneração da quádrica em um único ponto.E procurar degenerações é com a gente né. Aqui, novamente, a ideia é simplificar a equação.

Passo 2

Completando os quadrados:

x 2 + 3 y 2 + 2 z 2 + 2 k x + 4 k z + 9 = 0

x 2 + 2 k x + k 2 + 3 y 2 + 2 z 2 + 4 k z + 2 k 2 + 9 = k 2 + 2 k ²

x + k 2 + 3 y 2 + 2 z + k 2 = 3 k 2 - 9

Fazendo a substituição:

x 2 = x 1 + k

z 2 = z 1 + k

Temos:

x 2 + 3 y 2 + 2 z 2 = 3 k 2 - 9

Todos os termos da esquerda são ≥ 0 . Então, para que a solução seja única, devemos ter:

3 k 2 - 9 = 0

k = ± 3

Resposta

e   k = 3 ou k = - 3

Exercício Resolvido #10

P3-MAT2458-USP. Ano: 2011. Questão 6

Passo 1

Vamos analisar aqui a influência da cônica em b . Porém, invés de tentarmos simplificar a equação, o que daria muitas contas, vamos achar as degenerações e depois usar o método do Δ .

Passo 2

Vamos buscar possíveis degenerações resolvendo a equação para y : Δ B h a s k = 4 b 2 x ² - 3 3 x 2 - 6 x + 3 = 4 [ b 2 - 9 x 2 + 18 x - 9 ]

Observe que o termo de Δ B h a s k não é um quadrado perfeito, independentemente de b , já que o termo independente é negativo: - 9 .

Daí já podemos concluir que (III) é falso, já que não existem degenerações.

Passo 3

Agora vamos aplicar o método do Δ (não confunda o Δ = B 2 - 4 A C com o Δ B h a s k ):

Δ = 4 b 2 - 4.3 . 3 = 4 b 2 - 36

Analisando a função de 2º grau vemos que:

b < - 3 ou b > 3 ⇒ Δ > 0

b = - 3 ou b = 3 ⇒ Δ = 0

- 3 < b < 3 ⇒ Δ < 0

Assim, lembrando que não há degenerações:

b < - 3 ou b > 3 ⇒ Hipérbole

b = - 3 ou b = 3 ⇒ Parábola

- 3 < b < 3 ⇒ Elipse

Logo (I) é verdadeiro e (II) é falso.

Resposta

( b ) Apenas a afirmação (I) é verdadeira.

Exercícios de Livros Relacionados

Efetue a mudança de coordenadas (rotação de eixos) dada por x = a s − b t , y = b s + a t , onde a = c o s θ e b = s e n θ . Como fica, nas novas coordenadas s, t, a equação da circunferência x − m ²
Mostre que B ² - A C = 0 ² se, e somente se, A x ² + 2 B x y + C y ² = A (x + (B)/(A) y) ² ² ² ²
Para cada uma das equações abaixo, identifique detalhadamente a curva que ela define e a mudança de coordenadas que permitiu essa conclusão. f )3 x 2 + 6 x y+3 y 2 - 9 x - 6 y +6=0
Para cada uma das equações abaixo, identifique detalhadamente a curva que ela define e a mudança de coordenadas que permitiu essa conclusão. a )36 x ²+24 x y+29 y ²-120 x+10 y-55=0 ² ²
Para cada uma das equações abaixo, identifique detalhadamente a curva que ela define e a mudança de coordenadas que permitiu essa conclusão. b )17 x 2 - 312 x y+108 y 2 -590 x - 120 y +688=0