Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 5.Problemas propostos - Ex. 19c

19. Determinar as equações paramétricas e representar graficamente a reta que passa por:

c) e é ortogonal ao mesmo tempo aos eixos e ;

Passo 1

Antes de iniciarmos a resolução vamos relembrar rapidamente do que estamos falando quando utilizamos o termo “equações paramétricas”, tudo bem? Essas equações, assim como discutido no capítulo em questão do Winterle, são equações que representam uma reta qualquer utilizando uma mesma incógnita (geralmente chamada de ) que recebe o nome de parâmetro. Esse termo cria nada mais, nada menos do que uma ligação entre as equações paramétricas, galera! Show!

Dado um ponto qualquer do tipo , através da equação vetorial da reta conseguimos extrair que:

Onde as equações paramétricas da reta são:

E essa é a ideia que vamos aplicar para resolver nossa questão! Como já temos o ponto , então basta que consigamos determinar o vetor direção relacionado ao parâmetro , ou seja:

Então bora que bora!

Passo 2

A questão diz que a reta passa pelo ponto e é ortogonal ao plano . Já que a reta é perpendicular (ou ortogonal) ao plano , isso quer dizer que a reta não possui componentes em e em , apenas em , ok? Sendo assim, nosso vetor direção pode ser escrito da seguinte forma:

Que é, basicamente, o vetor canônico! Agora que encontramos nosso vetor direção, basta utilizarmos a relação que discutimos no passo . Como nosso ponto é , então:

Logo, nossas equações paramétricas serão:

Passo 3

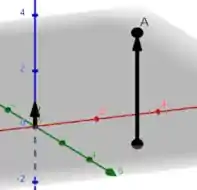
Agora que encontramos as equações paramétricas, se representarmos graficamente a reta que passa por e é ortogonal ao plano , teremos algo assim ó:

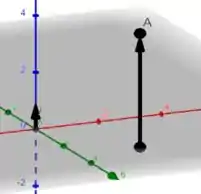
No qual o vetor direção é o que está à esquerda, enquanto o vetor maior que passa por é justamente a reta que queríamos esboçar! O eixo em vermelho é , o eixo em verde é e o eixo em azul é . Vale ressaltar também que como estamos em dimensões, então precisamos ter uma noção de perspectiva bem afiada, tudo bem? Massa!