Enunciado
Cálculo - Callioli - Álgebra Linear e Aplicações - Parte 2- Ed: 6º - Capítulo 5.2 - Ex. 5
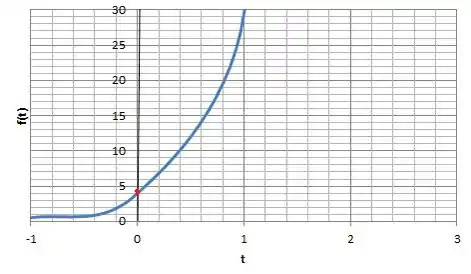
5. Achar uma função que esteja no núcleo do operador e cujo valor para seja . Fazer o gráfico dessa função.
Passo 1
Vamos lá... você pode estar se perguntando WTF é uma função que esteja no núcleo do operador tanãnãnã. Sei que não tem nada nessa seção explicando, maaaass tem um exemplinho na seção anterior que ajuda a entender isso e eu vou te explicar agora:
- pra uma função estar no núcleo do operador, devemos ter:
E pra isso acontecer, acredite em mim, a função tem que ter a seguinte cara (tem as provas disso na seção anterior, também)
Passo 2
Temos que pra , então:
Então a nossa equação fica, agora,
Passo 3
E pra função estar no núcleo do operado:
Bem... pra isso acontecer repare que precisa ser igual a 2, ne?
E a função final:
Passo 4
Falta o gráfico, ne´... vamos pra algumas dicas pra esboçar o gráfico:
- nós já temos o ponto quando , né... então marca ele:
- a função exponencial tem uma cara meio conhecida, (seria bom até você guardar porque vai aparecer bastanteee em várias outras matérias)... Maaass caso dê branco e não lembre... pode ir substituindo valores de t na função e ir achando pontos e depois só dá uma ligada nos pontos e TCHARAN... gráfico
Então é só traçar o gráfico com a cara da exponencial passando pelo ponto .
