A altura e a mediana relativas ao vértice do triângulo estão contidas, respectivamente, em e . Sendo , determine e .

Trocando o parâmetro da reta :

Então, encontrando um ponto genérico de cada reta:

Para encontrar o ponto em comum entre as duas retas, vamos igualar as coordenadas:

Da segunda equação, temos , substituindo na primeira:

Então

Para encontrar o ponto , que é a intersecção das retas, podemos substituir em ou em (vai resultar no mesmo ponto hehe). Substituindo em :

Agora vamos encontrar o ponto . Chamando , vamos começar encontrando a reta beleza? Sabemos que ela passa pelo ponto e que seu vetor diretor é:

Então, a reta é:

Como a reta é a altura do triângulo relativa ao vértice , ela deve ser perpendicular à aresta , certo? Pois a altura do triângulo sempre é perpendicular.

Então, o vetor diretor de deve ser perpendicular ao vetor diretor de , ou seja, o produto escalar entre eles deve ser 0:

Vamos guardar essa equação e achar mais algo que nos ajude hahaha

O ponto daquela figura no passo 1 é o ponto médio do segmento :

Mass, sabemos que esse ponto passa pela reta , que é a nossa mediana. Então, esse ponto também pode ser escrito como aquele ponto genérico lá do passo 2:

Igualando as duas equações de :

Igualando as coordenadas:

Temos 4 equações com 4 incógnitas e . Podemos formar um sistema:

Resolvendo esse sistema, encontramos:

Como chamamos o ponto de , temos:

E é isso aí, encontramos o e o que queríamos hahaha

Então, o que temos no espaço é isso aqui:

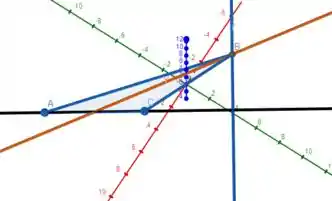
A reta azul é (a altura do triângulo), a reta laranja é (a mediana) e a reta preta é , perpendicular à reta .