Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 42c
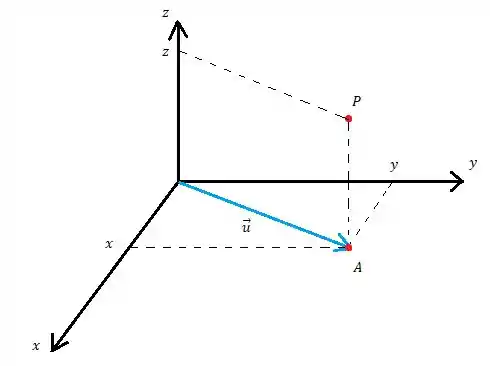
Apresentar o vetor genérico que satisfaz a condição:
paralelo ao plano ;
Passo 1
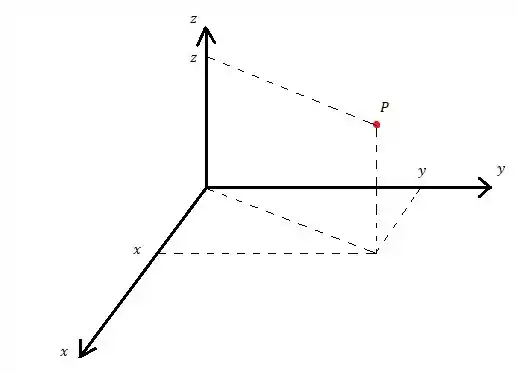
Vamos primeiro analisar o ponto genérico na figura abaixo:
Agora vamos ver o vetor que é:
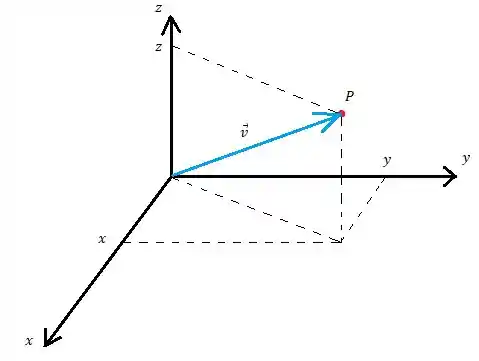
Esse vetor possui as três coordenadas , e , assim ele não é paralelo a nenhum plano.
Passo 2
Assim temos então que um vetor genérico que seja paralelo ao plano deve ter a coordenada de igual a zero, assim ele vai estar no plano sendo também paralelo a esse plano, então ele vai ser da forma:
Vamos ver isso melhor na figura:
Resposta
Exercícios de Livros Relacionados
Seja AA′ uma diagonal de um cubo e sejam B, C e D os vértices desse cubo que estão mais próximos de A. Mostre que AA′ é perpendicular a BC e BD e conclua que AA′ é perpendicular ao plano BCD. Mostre a
Ache quatro pontos A, B, C e D no espaço, cujas coordenadas sejam 1 ou 0, de modo que ABCD seja um tetraedro regular. Verifique que duas arestas opostas desse tetraedro são ortogonais.
Dados os pontos distintos A = (a, b, c), A ′ = (a ′, b′, c′) e o número d0, mostre que existem, na reta AA′, 0, 1 ou 2 pontos P tais que d (O, P) = d. Se existir exatamente um ponto P com d (O, P) = d
Dado um triângulo acutângulo A B C , mostre que existe um ponto O no espaço, tal que os Ângulos A Ô B ,A Ô CeB Ô C Ô Ô Ô são retos. Determine as medidas das arestas e da altura da pirâmide de base A B
Prove que uxv xw + vxw xu + wxu xv = 0 .