Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Parábola - Ex. 1

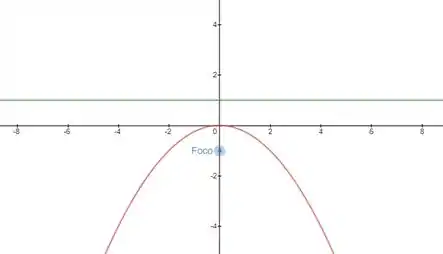
Para cada uma das parábolas dos Problemas de 1 a 10, construir o gráfico e encontrar o foco e uma equação da diretriz.

x 2 = - 4 y

Passo 1

Só de olhar a equação da parábola, temos 3 informações sobre ela:

  • Antes de tudo, vemos que nesse caso temos a equação de uma parábola com vértice na origem, certo? Porque temos ( x - 0 ) e ( y - 0 ) .
  • Agora é o seguinte, como quem está ao quadrado é o x , isso quer dizer que a parábola vai estar ao longo do eixo y
  • Além disso, deixando y positivo, multiplicando os dois lados por ( - 1 ) , temos 4 y = - x ² , como o número que multiplica x é negativo, essa parábola vai ter concavidade para baixo ;)

Passo 2

Uma parábola ao longo do eixo y tem formato

x 2 = 2 P . y

Sendo 2 P o número que multiplica y , no nosso caso temos

2 P = - 4

P = - 2

Vamos encontrar o foco da nossa parábola. Como o seu vértice está em V ( 0 ,   0 ) , ema tem foco

F 0 ,   0 + P 2

F ( 0 ,   0 - 2 2 )

F ( 0 ,   - 1 )

Passo 3

E agora vamos encontrar a nossa reta diretriz.

Ela é simétrica ao foco em relação à parábola. Então, como nosso foco está em - 1 no eixo y , a reta diretriz tem equação

y = 1

E essa é a nossa parábola:

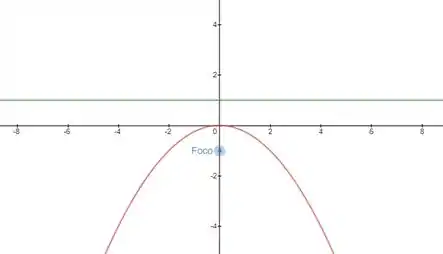
Resposta

F = ( 0 ,   - 1 )

Diretriz: y = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 21 a 26, ache uma nova equação para o gráfico da equação dada após uma translação de eixos para a nova origem, conforme está indicado. Trace os eixos originais e os novos e faça um e
Nos exercícios de 21 a 26, ache uma nova equação para o gráfico da equação dada após uma translação de eixos para a nova origem, conforme está indicado. Trace os eixos originais e os novos e faça um e
Nos exercícios de 21 a 26, ache uma nova equação para o gráfico da equação dada após uma translação de eixos para a nova origem, conforme está indicado. Trace os eixos originais e os novos e faça um e
Nos exercícios de 21 a 26, ache uma nova equação para o gráfico da equação dada após uma translação de eixos para a nova origem, conforme está indicado. Trace os eixos originais e os novos e faça um e
Nos Exercícios de 33 a 40, ache uma equação da parábola com as propriedades dadas. Faça um esboço do gráfico.34. Vértice em ( 1 ,- 3 ) ; diretriz y = 1 .