Para cada uma das parábolas dos Problemas de 1 a 10, construir o gráfico e encontrar o foco e uma equação da diretriz.

6)

Antes de colocarmos a mão na massa, precisamos saber se o eixo da parábola é o eixo dos ou . O bizu é o olhar o carinha que está elevado ao quadrado. Vamos fazer um resuminho:

- Se for o , a forma reduzida da parábola é , o foco é dado por e a equação da diretriz é dada por .

- Se for o , a forma reduzida da parábola é , o foco é dado por e a equação da diretriz é dado por .

Agora, já sabemos tudo que deveríamos! A equação dada no enunciado é , como quem está elevado ao quadrado é o , o eixo da parábola é o eixo dos . Assim, basta compararmos essa equação com a sua forma reduzida que vai ser dada por :

Por comparação, conseguimos determinar o valor de :

Com o valor de em mãos, fica fácil acharmos o foco e uma equação da diretriz:

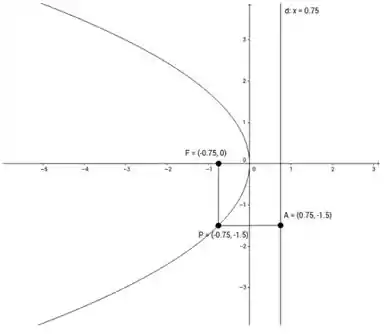
O foco vai ser dado por:

Já a equação da diretriz vai ser dada por:

Por fim, com o auxílio do Geogebra, nós construímos o nosso gráfico: