Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Parábola - Ex. 49b
Utilizar a definição para encontrar uma equação da parábola de foco e diretriz dados:
Passo 1
E aí, tudo joia?
Nesses casos aqui, uma boa ideia é a gente fazer o esboço da parábola primeiro pra entender o que tá acontecendo. Primeiro repare que a diretriz é , beleza?
Olha o gráfico:
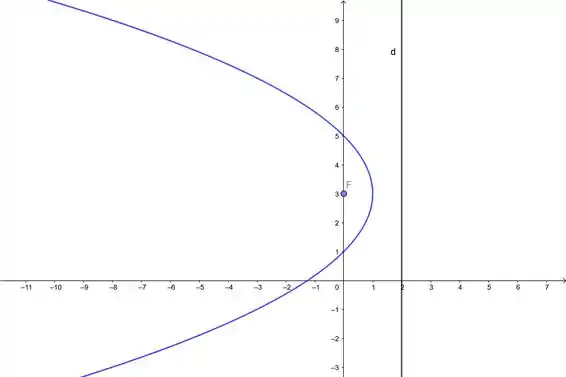
Passo 2
Beleza! Daqui a gente viu que a parábola tem eixo focar paralelo ao eixo , porém a parábola tá virada pra esquerda, então nosso vai ficar negativo. Vai ser dessa forma aqui:
Onde é o vértice, e é a distância do foco à diretriz.
É facinho de ver ali que .
E o vértice, que tá ali no meio do caminho, é:
Juntando essas informações, a gente joga na fórmula geral ali de cima...
Passo 3
Vamos ficar com:
Prontinho! Essa é a equação da parábola😉
Resposta
Exercícios de Livros Relacionados
45. Prove que, sobre uma parábola, o ponto mais próximo do foco é o vértice.
44. Um arco parabólico tem uma altura de 20 m e uma largura de 36 m na base. Se o vértice da parábola estiver no topo do arco, a que altura acima da base ele terá 18 m de largura?
51. Se os eixos forem transladados para uma nova origem tendo coordenadas ( h , k ) , mostre que após a translação a equação y = s e nx torna – se y ' = As e nx ' + B cos x ' + C , onde A, B e C são
49. A equação da diretriz de uma parábola é x + y = 0 e se foco está no ponto ( 1 ,1 ) . Ache (a) a equação do eixo da parábola, (b) as coordenadas do vértice e (c) 0 comprimento do latus rectum.
46. Suponha que a órbita de determinado cometa seja uma parábola com o Sol no foco. Quando o cometa está a 100 milhões de quilômetros do Sol, o ângulo entre o eixo da parábola e a reta do Sol até o co