Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Hipérbole - Ex. 35

Em cada um dos problemas de 14 a 37, determinar uma equação da hipérbole que satisfaça as condições dadas. Esboçar o gráfico.

Focos F 1 - 1 , - 5 e   F 2 ( 5 , - 5 ) e que seja hipérbole equilátera.

Passo 1

Opaaa! Tudo joia?

Bom, a questão nos deu os focos F 1 - 1 , - 5   e     F 2 ( 5 , - 5 ) e nos disse que a hipérbole é equilátera.

Lembra de triângulo equilátero? Ele tinha os lados iguais, certo? Aqui é a mesma coisa, hipérbole equilátera quer dizer que ela tem os eixos do mesmo tamanho.

Vamos ver um esboço desses focos?

Já deu pra imaginar como vai ser a hipérbole?

O eixo é paralelo ao eixo x , e já que a distância de um foco ao outro é 6 , o centro fica ali em ( 2 , - 5 ) , certo?

Passo 2

Continuando, como já dissemos que ela é equilátera, os eixos têm o mesmo tamanho, então a = b , logo se a gente usar a relação:

c 2 = a 2 + b 2

A gente vai achar a medida dos eixos, já que sabemos que 2 c = 6 → c = 3 .

3 2 = a 2 + a 2

9 = 2 a 2

a 2 = 9 2

a = 9 2 = 3 2 = 3 2 2

Beleza, nossos vértices então são:

A 1 2 - 3 2 2 ,   - 5       e     A 2 2 + 3 2 2 ,   - 5

Passo 3

Como o eixo é paralelo ao eixo x , a equação é da forma:

x - h 2 a 2 - y - k 2 b 2 = 1

x - 2 2 9 / 2 - y + 5 2 9 / 2 = 1

Pra deixar da forma geral, vamos desenvolver essa expressão...

x 2 - 4 x + 4 - y 2 + 10 y + 25 9 / 2 = 1

x 2 - 4 x + 4 - y 2 - 10 y - 25 = 9 2

2 x 2 - 8 x + 8 - 2 y 2 - 10 y - 50 = 9

2 x 2 - 2 y 2 - 8 x - 10 y - 51 = 0

Passo 4

Juntando essas informações, a gente monta nosso esboço...

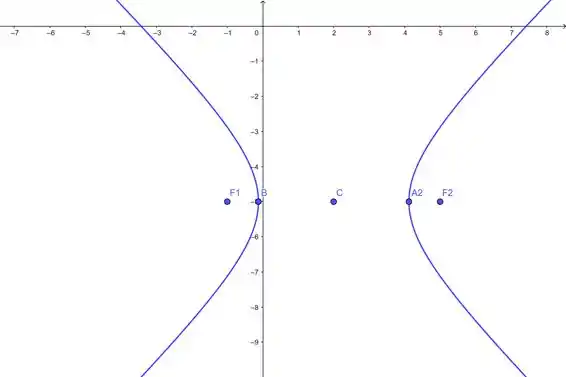
Prontinho! 😉

Resposta

2 x 2 - 2 y 2 - 8 x - 10 y - 51 = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam T = ( h , k ) um ponto da hipérbole H : x 2 a 2 - y 2 b 2 = 1 e A e B os pontos em que a reta tangente a hipérbole em T intercepta as assíntotas. ( a ) Escreva as coordenadas de A e B em termos
Obtenha equações das retas que contém o ponto P = ( 1 , - 9 ) e são tangentes a hipérbole de equação 3 x 2 - y 2 = 39 . Determine os pontos de tangência e a reta normal em cada um deles.
Seja H a hipérbole de equação reduzida - x 2 / a 2 + y 2 / b 2 = 1 . Calcule as distâncias de um ponto genérico X = x ,y de H aos focos, em função de y .
São dados, em cada caso, o parâmetro geométrico a e os focos de uma hipérbole. Obtenha uma equação algébrica de segundo grau em x e y que todo ponto x , y da hipérbole deve satisfazer. a = 3F 1 = 3 ,-
Calcule, em cada caso, a excentricidade da hipérbole H . 4 x 2 - y 2 = 16 . x 2 - 2 y 2 + 8 = 0 . O triângulo F 1 B 2 F 2 é retângulo. As diagonais do retângulo fundamental formam ângulos de 60 ° . Os