Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 16.Exercício - Ex. 2
Calcule em cada caso, usando a informação dada sobre as retas
a) e são paralelas.
b) e são paralelas a um mesmo plano.
c) e são concorrentes.
d) e t são coplanares.
e) e são reversas.
Passo 1
Primeiro vamos encontrar uma equação da reta :
Da primeira equação:
E na segunda equação:
Então a equação da reta é:
Passo 2
Agora vamos encontrar uma equação para :
Somando as duas equações:
Substituindo na equação de cima:
Então a equação da reta é:
Além disso, a equação vetorial de é:
Agora vamos começar :)
Passo 3
a) Para que sejam paralelas, seus vetores diretores devem ser múltiplos, ou seja:
Igualando as coordenadas:
Da terceira equação temos , e na primeira temos , então, para que as retas sejam paralelas, precisamos ter:
Passo 4
b) Para que as retas sejam paralelas a um mesmo plano, os seus vetores devem ser LD, certo? Ou seja, um deles deve ser combinação linear dos outros dois:
Devemos ter .
Igualando as coordenadas:
Resolvendo esse sistema, encontramos:
Passo 5
c) Se observarmos as equações de e , vemos que as duas passam pelo mesmo ponto: , certo? Então já temos meio caminho andado pra elas serem concorrentes hehe
Agora, só falta os vetores diretores delas serem LI, porque se forem LD estaremos falando de duas retas iguais não é?
Vamos ver qual o valor de que faz os vetores diretores serem LD, e aí para diferente desse valor, eles serão LI ok?
Igualando as coordenadas:
Na segunda linda, temos , mas na terceira, temos . Como encontramos valores diferentes, isso quer dizer que esse sistema não é possível, ou seja, não tem como os vetores serem LD.
Portaaanto, pra qualquer valor de os vetores serão LI e as retas serão concorrentes.
Passo 6
d) Duas retas coplanares são paralelas distintas ou concorrentes, não é?
Primeiro vamos ver a condição para que os vetores diretores das duas retas sejam paralelos:
Igualando as coordenadas:
Na primeira linha, temos , mas na terceira temos , então, esse sistema não é possível e os vetores diretores não serão paralelos pra nenhum valor de .
Então elas só podem ser coplanares se forem concorrentes, para verificar isso, vamos fazer o determinante:
Para que elas sejam concorrentes:
Abaixo vemos as retas concorrentes com seu plano em comum para :
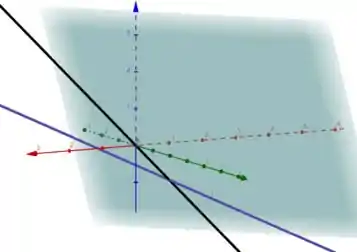
Passo 7
e) Para e serem reversas, seus vetores diretores primeiramente devem ser LI
Para , os vetores são LD, pois são múltiplos.
Então, para que os vetores sejam LI, já sabemos que .
Agora temos que calcular o determinante para garantir que as retas sejam reversas, e não concorrentes ok?
O determinante vai ter as linhas , sendo da equação de e da equação de , portanto .
Para as retas serem reversas, esse determinante deve ser diferente de 0:
Logo, para que as retas sejam reversas pode assumir qualquer valor, menos 0 e 1 ;)
Resposta
a)
b)
c) Qualquer valor de
d) Não existe que satisfaça
e)