Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 33
Sejam a superfície esférica de centro e raio , e , o plano tangente a em . Prove que todos os pontos de , exceto , pertencem ao semi-espaço aberto de origem que contém (isto é, não os separa de ).
Calcule o raio de uma superfície esférica tangente aos três planos coordenados que contém o ponto
Passo 1
Da questão anterior nós vimos que um plano tangente respeita a seguinte equação vetorial:
E basicamente o que essa questão pede é que provemos que o plano não corta a esfera em nenhum ponto (a não ser o ponto de tangência ) de modo a ter um ponto da esfera que está numa metade desse corte feito pelo plano e o centro no outro. Tal como a imagem embaixo.
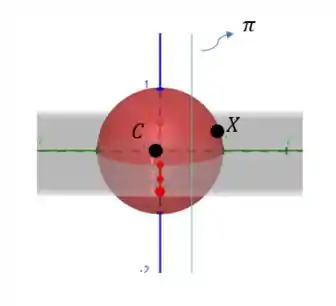
Provar que essa imagem é absurda!
Vamos por exemplo considerar que temos uma esfera e temos um plano tangente em ou seja o plano tangente será em :
Se por um acaso quisermos saber o comportamento da equação no ponto nós teremos:
E no ponto , que pertence a esfera.
Isso é, se o ponto está antes do plano o resultado da multiplicação , dará menor que e se tiver depois ele dará maior que e se ele está depois a multiplicação dará maior que .
Passo 2
De maneira mais genérica, tomemos um centro de círculo de centro , um ponto de tangência em e um em diferente de , nós teremos então uma expressão igual a:
E como a equação da esfera é algo como:
Então só temos uma possibilidade para ser igual a , que é , e como supomos , então isso é um absurdo e isso não ocorrerá. Somente quando .
Passo 3
Na letra nós teremos que para a esfera ser tangentes aos três planos ordenados então , tal como visto no exercício e se ele contém o ponto então pela parte sabemos que:
Pois o plano tangente separa as coordenadas positivas das negativas nos três planos, logo a esfera somente terá coordenadas positivas em , somente negativas em e somente positivas em .
Então aplicando o ponto em uma esfera de centro nós teremos:
Cujas raízes serão: e , e esses serão os valores dos raios da esfera.
A superfície esférica pode ser vista abaixo:
