Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 53

Obtenha equações da circunferência de centro que determina uma corda de comprimento 8 sobre a reta interseção dos planos e .

Passo 1

Bom, se queremos a equação de uma circunferência, precisamos de duas coisas: a equação de um plano que contém a reta e o centro , e a equação de uma superfície esférica.

Para ajudar a nossa visualização, vamos começar fazendo um esboço no plano da circunferência e do que está acontecendo. Vejamos abaixo:

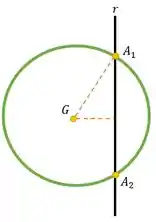
A reta é a reta dada pela interseção dos dois planos. O segmento é a corda de comprimento 8 dada no enunciado da questão. Ao descobrirmos a equação da reta, vamos construir um plano que contém a reta e o ponto .

E para construir a superfície? Como faremos? Vamos analisar do final pro início. Precisamos de um centro e raio. Podemos assumir que o centro será o centro da circunferência . Já o raio da circunferência será o raio da superfície.

Passo 2

Primeiro, vamos calcular a reta . Para isto, vamos resolver o seguinte sistema:

Logo,

Portanto, a reta será:

Então, se chamarmos de e multiplicarmos o vetor diretor por 2 para eliminar a razão, temos:

Passo 3

Agora, vamos compor nosso plano . Vamos montar um vetor , sendo pertencente a . Portanto,

Logo,

Portanto o plano tem o seguinte formato:

Substituindo as coordenadas de para descobrir o valor de , temos:

Portanto, o plano é:

Passo 4

Agora, nosso objetivo será descobrir o raio da circunferência Para isto, vamos precisar descobrir a distância de até (e automaticamente, ), que é exatamente o raio da circunferência.

Novamente, vamos voltar ao desenho lá do Passo 1.

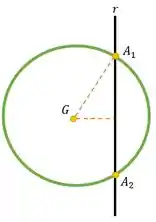
Conseguem ver o triângulo retângulo de lados , e ? Vamos utilizar o teorema de Pitágoras para descobrir o raio . Mas, antes disto, vamos calcular a distância . Portanto,