Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 76
Calcule a medida angular entre as retas tangentes à hipérbole de equação nos pontos .
Passo 1
Desejamos encontrar o valor do ângulo entre as retas tangentes à hipérbole mencionada. Pois bem, como ambos os pontos pertencem à nossa hipérbole (pode-se verificar isso substituindo as coordenadas e na equação da hipérbole e verificando a igualdade) podemos utilizar o jeito prático de se calcular uma reta tangente à hipérbole que é
Onde são as coordenadas do ponto de tangência e vem da equação da elipse mesmo. Sendo assim, vamos ter as seguintes equações
Para o ponto vamos ter
Passo 2
Para avaliarmos o ângulo entre essas retas vamos plotar as duas juntas para que possamos visualizar mais facilmente. Dessa forma, temos
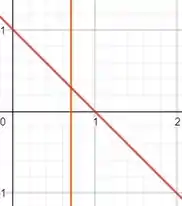
Ou seja, temos uma reta vertical e uma reta com inclinação de , portanto, a medida angular para as retas entre si é de .