Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 19a

Nos casos em que a equação dada descreve uma hipérbole de focos em algum dos eixos coordenados, especifique-o e calcule a distância focal e as medidas do eixo transverso e conjugado. Faça alguns esboços, a mão livre e com o auxílio do computador, para comparar.

  1. 9 x 2 - 4 y 2 = 36
  2. 9 x 2 25 - y 2 + 9 = 0
  3. x 2 + 2 y 2 = 1
  4. - m 2 x 2 + 9 y 2 = 36 ,   m > 0
  5. 25 x 2 - 100 y 2 = 0
  6. 5 x 2 - 9 y 2 - 45 = 0
  7. x 2 - y 2 + 1 = 0
  8. x sen ⁡ φ 2 - y cos ⁡ φ 2 + 1 = 0   ( 0 < φ < π / 2 )  

Passo 1

Para resolvermos esta questão, temos que colocar as equações na seguinte forma:

x 2 p + y 2 q = 1

Se os valores p e q tiverem sinais trocados, teremos uma hipérbole.

Os focos estarão no eixo relativo à variável positiva (denominador positivo). Por exemplo, se tivermos p > 0 e q < 0 , os focos estarão em O x e não em O y .

Pronto, a ideia da questão é tentar colocar as equações dadas exatamente na forma acima. Se conseguirmos, temos uma hipérbole. Caso contrário, não temos uma hipérbole.

Então, vamos começar a adaptar a nossa equação. Portanto,

9 x 2 - 4 y 2 = 36

9 x 2 - 4 y 2 36 = 36 36

x 2 36 9 + y 2 36 - 4 = 1

x 2 4 + y 2 - 9 = 1

Pronto, como p = 4 > 0 e q = - 9 < 0 , temos sim uma hipérbole! Em especial, como p > 0 , os focos estão localizados no eixo O x .

Passo 2

Agora, iremos determinar os outros parâmetros pedidos pela questão. Mas, antes disto, vamos determinar os parâmetros geométricos da hipérbole.

Logo,

a = p = 4 = 2

b = - q = 9 = 3

c = a 2 + b 2 = 4 + 9 = 13

Agora sim podemos calcular o que a questão nos pede.

A distância focal tem comprimento 2 c . Portanto, 2 13 .

Para uma hipérbole com focos no eixo O x , o eixo transverso tem comprimento 2 a . Portanto, 4. Já o eixo conjugado tem comprimento 2 b . Logo, 6 .

Passo 3

A questão também nos pede para compararmos o esboço a mão livre e com o uso de softwares. Entretanto, aqui será feito somente o esboço da hipérbole através de softwares.

Desta forma, temos:

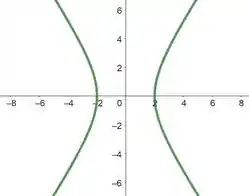
Resposta

Os focos estão no eixo O x .

A distância focal tem comprimento 2 13 . O eixo transverso tem comprimento 4 e o eixo conjugado tem comprimento 6 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Focos F ( 0 , ± 5 ) , comprimento do eixo imaginário 4.
Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Focos F 1 ( - 1 , - 5 ) e F 2 ( 5 , - 5 ) , hibérbole equilátera.
Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Vértices em ( 5 , - 2 ) e ( 3 , - 2 ) , um foco em ( 7 , - 2 ) .
Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Vértices em ( 5,5 ) e ( 5 , - 1 ) , excentricidade e = 2 .
Em cada um dos problemas 11 a 24, determinar a equação da hipérbole que satisfaz as condições dadas.Centro C ( 2 , - 3 ) , eixo real paralelo a 0 y , passando por ( 3 , - 1 ) e ( - 1,0 ) .