Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 19.Exercício - Ex. 21

Bom pessoal, vamos começar com um desenho da situação, um cubo de lado e uma diagonal.

E vamos colocar a origem do sistema de coordenadas em um dos vértices do cubo:

Uma coisa é importante: não faz diferença qual diagonal você está pegando

Se trocássemos aquele por outro, era só “girar o cubo” e o sistema de coordenadas, e daria pra chegar nessa mesma situação!

Como o lado é , vamos escrever as coordenadas dos pontos e :

Então vamos começar encontrar a equação da reta que contém a diagonal. Essa reta é paralela ao segmento .

Então o vetor diretor da reta é:

E como a constante não faz diferença no vetor diretor, vamos usar só:

Tá, do que a gente precisa para encontrar o ângulo entre a reta e um plano ?

Bom, se a reta tem vetor diretor e um plano tem um vetor normal , o ângulo entre e é:

Então a gente precisa do vetor normal ao plano.

Como falamos antes, por simetria, o ângulo que a reta faz é o mesmo com todos os planos.

Vamos procurar o vetor normal a esse plano aqui:

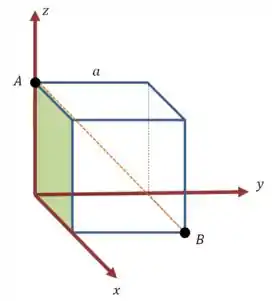
Pelo desenho, o vetor normal ao plano é o eixo , ou seja, é esse vetor unitário aqui:

Agora é só usar a fórmula de cima:

Primeiro vamos fazer o produto escalar:

E as normas são:

Substituindo na fórmula:

Melhorando um pouco:

Ou seja, o ângulo é:

O ângulo é .