Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 10c
Nos casos em que o lugar geométrico é uma superfície esférica determine o centro e o raio.
(a) Lugar geométrico dos pontos de tais que a soma dos quadrados de suas distâncias aos eixos coordenados seja .
Passo 1
Vamos tentar resolver esse problema só usando um pouco de álgebra.
Como se calcula a distância de um ponto até um eixo coordenado? Vamos fazer um desenho para entender:
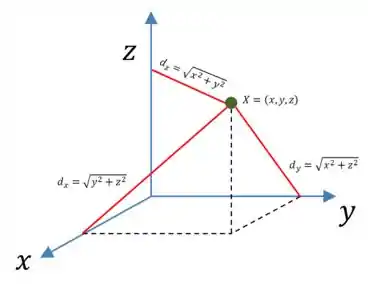
Ok, então temos essas três fórmulas, todas encontradas usando o teorema de Pitágoras.
Passo 2
O enunciado pediu que a soma dos quadrados dessas distâncias seja , então:
Substituindo com as fórmulas:
Tirando essas raízes quadradas:
E arrumando um pouco:
E dividindo tudo por :
Passo 3
Ok, já simplificamos bastante. Agora já dá pra encontrar o centro e o raio da esfera.
Lembrando que se uma esfera tem centro e raio , a equação é:
Então, olhando para a equação:
Podemos ver que:
E o raio é:
Resposta
O centro da esfera é e o raio é .