Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 14
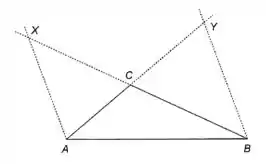
Dado o triângulo , sejam e os pontos tais que e (Figura).
(a) Prove que se, e somente se, .
(b) Mostre que, se é interior ao lado e é interior ao lado , então as retas e são concorrentes.
Passo 1
Vamos começar encontrando expressões simples para e . Dê uma olhada no desenho para entender isso!
E vamos reescrever e também:
Substituindo isso nas equações de cima:
E usando as relações e :
Passo 2
(b) Agora vamos lembrar do seguinte: um ponto é interior a um segmento se existe algum que satisfaça:
Isso é uma forma mais complicada de dizer que um ponto interior a um segmento, é um ponto que está no segmento.
Então se, no nosso triângulo, é interior a :
E se é interior a :
Vamos representar isso em um desenho:
Daqui podemos escrever que:
E se e forem paralelos, então tem que existir tal que:
Ou seja:
Como e , esses três vetores nunca podem ser paralelos. Então a solução exigira que:
Mas e são concorrentes, porque são lados de um triângulo. Então não existe solução para o nosso sistema, e então os lados não podem ser paralelos.
Portanto, e são concorrentes: não existe tal que:
Resposta
(a) Demonstração.
(b) Demonstração.