Dados o ponto e a superfície esférica de centro e raio , sejam e uma reta que contém e intercepta nos pontos e (eventualmente, iguais). Seja o simétrico de em relação a .
(a) Prove que
(b) Exprima e como combinação linear de , e mostre que . Conclua que não depende de , mas apenas de e . Esse número chama-se potência de em relação a .
(c) Mostre que o módulo da potência de em relação a é , e que ela é positiva se é exterior a , negativa se é interior, e nula se pertence a .
(d) Se e S: , mostre que a potência de em relação a é , valor do primeiro membro se .
(e) Calcule a potência de em relação a e obtenha dois pontos cuja potência em relação a essa mesma superfície seja .
(f) Dado o número real , descreva o lugar geométrico dos pontos de cuja potência em relação a é .
Passo 1
(a) Vamos tentar resolver o primeiro item com uma demonstração geométrica:
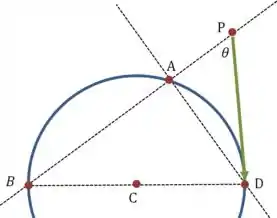
Podemos escrever uma relação entre e :
E os vetores e são paralelos, então, pela definição do produto escalar:
Substituindo a expresão que encontramos para :
Mas também é o ângulo que forma com , então esse termo do lado direito é a própria definição do produto . Ou seja:
Passo 2
E quando estiver no interior da esfera? Aí o lado esquerdo da equação vai ser:
Mas o ângulo que nós entre e vai ser tal que:
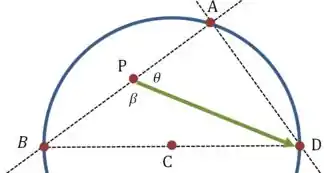
Ou seja:
Então, voltando na equação lá de cima:
E substituindo :
Mas é justamente o ângulo formado por e , então essa é a definição do produto escalar entre eles:
Beleza, provamos essa igualdade para os dois casos!
Passo 3
(b) Agora vamos escrever como combinação linear de , :
E fazendo o mesmo para :
Perceba que é um raio da esfera! E como está é simétrico a , só precisamos mudar o sentido desse raio para chegar até o ponto . Veja o desenho lá em cima!
Agora vamos fazer o produto escalar que o enunciado pediu:
O produto escalar de um vetor por ele mesmo é simplesmente o quadrado da sua norma, então:
Mas o próprio enunciado diz que a distância entre e é e é um raio da esfera, então:
Mas nós vimos lá em cima que:
Então:
Essa é a tal “potência de em relação a ”. Como esperado, ela não depende do raio .
Passo 4
(c) Agora queremos mostrar que o módulo dessa “potência” aqui:
É igual a . Bom, pela própria definição do produto escalar:
Então:
Conforme a gente viu no passo , quando o ponto é exterior à esfera, então:
E nesse caso a potência é positiva. E quando o ponto é interior à esfera, então:
E nesse caso a potência é negativa!
Passo 5
(d) Quando temos uma esfera de raio e centro com essa equação geral:
E são as coordenadas de um ponto qualquer, então essa expressão:
É igual a:
No nosso caso temos , então:
Que é justamente a potência do ponto em relação à esfera .
Passo 6
(e) Agora queremos calcular a potência do ponto em relação a uma esfera que tem essa equação geral:
Nesse caso só precisamos substituir no termo do lado esquerdo:
E o resultado dessa expressão é .
Para encontrarmos dois pontos cuja potência em relação à esfera dê , podemos começar escrevendo esse ponto da seguinte forma geral:
Então, substituindo na fórmula:
Agora é só igualar isso a e resolver a equação do segundo grau:
E então as duas raízes são:
E então os dois pontos são:
Passo 7
(f) Vamos lembrar da fórmula para a potência de um ponto em relação a :
Lembrando que é o raio da esfera e é o raio da esfera formada pelo ponto :
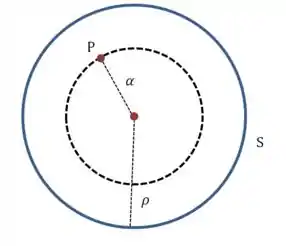
Ou seja, todos os pontos que tem potência estão em uma esfera de raio . Voltando na expressão de cima:
Então o lugar geométrico dos pontos com potência é uma esfera com centro em e raio .
Uma obsevação importante: nos casos em que essa raiz quadrada for negativa:
Então o lugar geométrico formado pelos pontos de potência é vazio!
Resposta
(a) Demonstração.
(b) Demonstração.
(c) Demonstração.
(d) Demonstração.
(e) A potência é . Dois exemplos seriam e .
(f) O lugar geométrico é uma superfície esférica de raio e centro em . Ou, se , o lugar geométrico é vazio.