Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 23.Exercício - Ex. 8f
Identifique a cônica e, quando for o caso, obtenha seus parâmetros geométricos (, , ou ) e determine, em relação ao sistema inicial, os elementos geométricos principais: centro, focos, vértices, eixos, assíntotas, diretriz, etc.
(f)
Passo 1
(b) Agora queremos resolver essa equação aqui:
Nosso primeiro objetivo aqui vai ser se livrar desse termo misto, o .
O primeiro passo pra fazer isso é dar nome para os coeficientes na equação. Lembrando que a forma geral é:
E a ideia aqui é aplicar uma rotação de coordenadas dessa forma aqui:
Mas vamos usar as fórmulas que o livro demonstra para facilitar essa conta. A ideia é transformar essa equação em uma nova com essa forma aqui:
Ok, vamos em frente.
Passo 2
Para encontrar o ângulo da nossa rotação, vamos usar essa fórmula aqui:
No nosso caso:
E para descobrir os coeficientes e da nova equação, temos que primeiro encontrar o . Dá pra fazer isso usando essa fórmula:
Agora é só resolver esse sistema aqui para encontrar e (lembrando que só estamos aplicando fórmulas aqui! Elas valem para qualquer caso de rotação de coordenadas):
Substituindo com os nosso valores:
Somando as duas equações:
E substituindo isso na primeira equação:
Então por enquanto a nossa equação está assim:
Ah, e a constante não muda com a rotação, então:
Passo 3
Também calculamos que o ângulo de rotação é tal que:
Temos que usar isso para descobrir e .
Sabemos que , então:
Ou seja:
Passo 4
Agora que conhecemos esse valores podemos usar mais uma fórmula! Essa serve para calcular e :
Substituindo , e os valores que calculamos agora:
Então a nossa equação é:
Mas ainda podemos ajeitar um pouco.
Passo 5
Para melhorar essa expressão, vamos completar quadrados. Mas antes vamos agrupar alguns termos:
Agora dê uma olhada nesse produto notável:
Então:
Melhorando ainda mais:
Agora fica claro que é a equação de uma parábola! Vamos procurar algumas propriedades.
Passo 6
Lembrando que nós aplicamos essa transformação de coordenadas:
E nossa equação é:
Isso quer dizer que o vértice da parábola, no sistema de coordenadas novo, é:
Jogando isso na nossa transformação de coordenadas:
Então o vértice é:
A equação da parábola tem essa forma geral:
No nosso caso, (que cumpre o papel de ) está multiplicado por . Então o parâmetro é:
Agora veja esse desenho: a linha pontilhada é a parábola desenhada no sistema e a outra é a equação original:
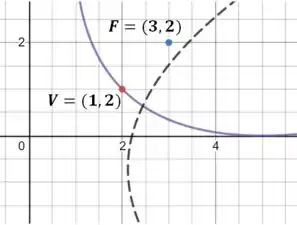
Resposta
A equação descreve uma parábola de equação .