Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Parábola - Ex. 54
Dados os sistemas de equações paramétricas:
Mostrar que eles representam parte de uma mesma parábola, esboçando o gráfico.
Passo 1
E aí, tudo joia?
Vamos colocar essas equações na forma geral?
Olha só:
Isolando o , a gente vai ter:
E substituindo na de baixo:
Essa é a equação da parábola, só que como o intervalo de é , é o trechinho onde é .
Passo 2
Vamos ver a outra agora, do mesmo jeito:
Temos que , então substituindo na de baixo temos:
Viu só? Deu a mesma equação da parábola! Ou seja, essas equações representam a mesma parábola!
O trechinho dessa aqui é onde , trazendo isso pra , é o trecho:
Prontinho! Provamos o que queríamos😉
Passo 3
Vamos ver o esboço da parábola:
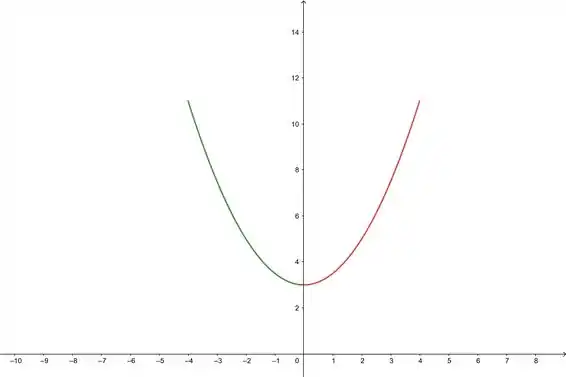
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Um espelho parabólico é obtido por rotação de uma parábola P em torno do seu eixo. Um raio luminoso parte do foco, atinge a superfície do espelho, e vai iluminar um ponto A de um anteparo. Determine a
São dados, graficamente, o foco e a diretriz de uma parábola, respectivamente F e r . Descreva um método de construção com régua e compasso:de pontos da parábola, baseado apenas na definição 22-16;da
Sejam P um ponto qualquer de uma parábola, distinto do vértice, R sua projeção ortogonal sobre o eixo da parábola, M e N , respectivamente, os pontos que esse eixo intercepta a reta tangente e a reta
Sejam P : y 2 = 4 p xp0 e P = h ,k . Prove que: Se P pertence à região focal da parábola, nenhuma reta que contém P é tangente a ela;Se P pertence à região côncava determinada pela parábola, existem d
Descreva a construção com régua e compasso de um ponto P da parábola, conhecidos a projeção ortogonal de P sobre o eixo P ' , o foco F e a diretriz r .