Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 2.Exercício - Ex. 10
10. Utilize o paralelepípedo da figura 2-9 (a) para determinar o vetor em cada caso:
a)
b)
c)
Passo 1
A figura 2-9 que ele cita é essa aqui:
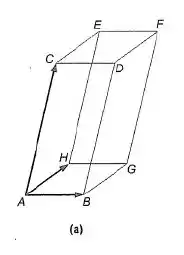
Para facilitar vou escrever os vetores iguais, para fazermos isso apenas pegamos os vetores paralelos.
Nossa ideia vai ser sempre escrever em função de e
Passo 2
Vamos começar com a letra a)
Vamos antes de tudo trocar os sinais do que está negativo!
Reescrevendo, temos:
Desenhando esses vetores na figura, temos:
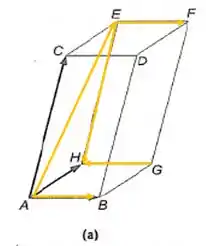
A soma deé dada pelo vetor que .
Já a soma do vetor é da dada pelo vetor .
Reescrevendo a soma, temos:
Passo 3
b) Na letra B temos
Que podemos reescrever da seguinte forma
Jogando tudo na nossa equação para
Passo 4
Já na letra C temos que fazer
E aí reescrevemos da seguinte forma
Então
Belezinha? :)
Resposta
a)
b)
c)
Exercícios de Livros Relacionados
Sugestão para os próximos 2 exercícios: Considere o paralelogramo A B C D . Seja U =A B → e V =A D → . Observe que as diagonais do paralelogramo são U + V e U - V .
Mostre que o angulo inscrito em uma semicircunferência é reto.
O produto vetorial é associativo? Justifique a sua resposta. (Sugestão: experimente com os vetores i → , j → , k → )
Sabe-se que o vetor X é ortogonal a i → + j → e a - i → + k → , tem norma 3 e sendo θ o ângulo entre X e j → , tem-se cos θ0 . Ache X .
Mostre que (c) U . Vxα W 1 + β W 2 = α U . VxW 1 + β U . VxW 2 ;