Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 20.Exercício - Ex. 20
Deduza a fórmula abaixo:
(a) raciocinando assim: se , então (recorde a condição (b) da Definição 9-12);
(b) aplicando o Teorema de Pitágoras ao triângulo da figura abaixo:
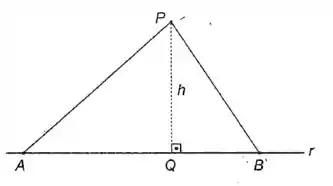
Passo 1
(a) Vamos seguir a sugestão do enunciado. A condição (b) da Definição 9-12 diz que se:
Então:
Vamos fazer um desenho para representar isso:
E a sugestão do enunciado foi considerar que , ou seja:
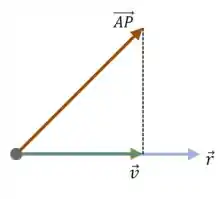
Isso quer dizer que . Só precisamos fazer mais um desenho para perceber isso:
A linha pontilhada é a distância entre o ponto e a reta , e também é a norma do vetor .
Passo 2
Agora vamos representar tudo isso algebricamente, para tentar chegar na fórmula do enunciado.
A fórmula em que queremos chegar é essa aqui:
Pensando geometricamente, o que isso tem a ver com a fórmula que vimos até aqui?
Bom, a norma do produto vetorial entre dois vetores é a área do paralelogramo formado por eles, ou seja:
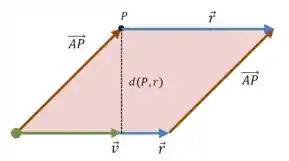
O produto vetorial representa essa área vermelha aí de cima. Mas outra forma de escrever essa área é usando o clássico “base vezes altura”, então:
Já que o comprimento do vetor é a base do paralelogramo e a distância é a altura.
Isso quer dizer que:
E então:
Pronto! Demonstramos a fórmula.
Passo 3
(b) Agora o enunciado quer a mesma demonstração, mas utilizando o teorema de Pitágoras:
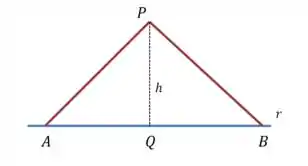
Aplicando o teorema de pitágoras ao triângulo :
A altura é a distância que queremos encontrar, então vamos isolar:
Mas o é a projeção do vetor na direção da reta . Como eles formam um ângulo que podemos chamar de , podemos escrever:
Então:
E lembrando que :
Tirando a raiz quadrada dos dois lados:
Agora vamos lembrar que a norma do produto vetorial é:
Ou seja:
Substituindo na equação de cima:
E como é um vetor diretor da reta , isso é a mesma coisa que:
Que é exatamente a fórmula que queríamos demonstrar!
Resposta
(a) Demonstração.
(b) Demonstração.