Determine o foco, o vértice, o parâmetro e a diretriz da parábola e faça um esboço.
- .
- .
- .
- .
- .
- .
Passo 1
Sabemos que, de modo geral a equação de uma parábola pode ser dada por
Vamos tentar reduzir as equações dadas a alguma dessas.
Passo 2
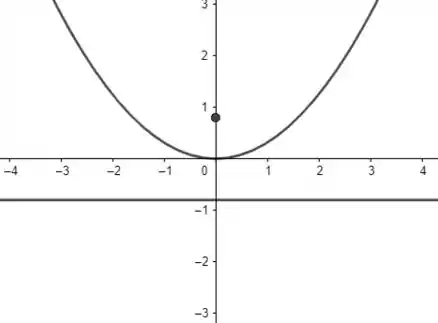
- Temos e comparando com , vemos que . O vértice é , o foco é e a diretriz a reta .
- Podemos reescrever a equação como . Comparando com , vemos que . O vértice é , o foco e a diretriz .
- Podemos reescrever a equação como . Comparando com , vemos que . O vértice é , o foco e a diretriz .
- Podemos reescrever a equação como . Comparando com , vemos que . O vértice é , o foco e a diretriz .
- Podemos reescrever a equação como . Comparando com , vemos que . O vértice é , o foco e a diretriz .
- Podemos reescrever a equação como . Comparando com , vemos que . O vértice é , o foco e a diretriz .
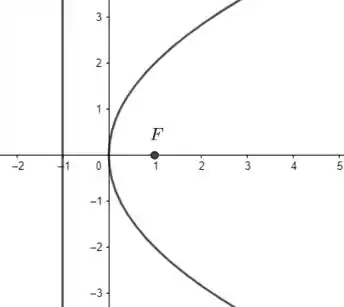
Passo 3

Passo 4
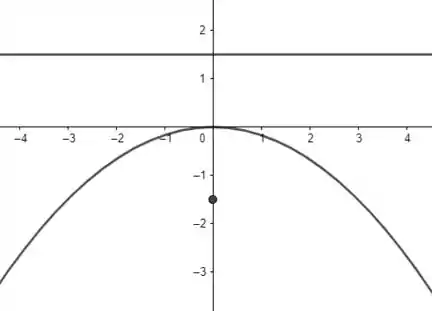
Passo 5
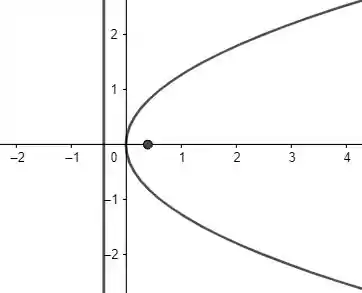
Passo 6
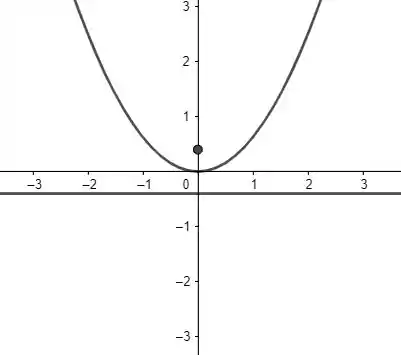
Passo 7
Resposta
Ei, a resposta está no passo a passo :)