Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 15.Exercício - Ex. 7

O detonador de uma bomba está localizado no ponto . Para provocar a explosão, acende-se a extremidade de uma haste combustível paralela ao vetor , cuja extremidade toca o ponto inicial de um rastilho de pólvora retilíneo que termina no detonador. Sabendo que o fogo se propaga com velocidade unitária na haste e no rastilho e que este está contido no plano , mostre que a explosão ocorre entra 3 e 4 segundos após o início do processo. O sistema de coordenadas é ortogonal.

Passo 1

Eu sei que esse exercício parece confuso hahaha mas vamos por partes pra ficar bem simples:

Pelos dados do exercício, sabemos que o ponto e o ponto estão no plano (“cuja extremidade toca o ponto inicial de um rastilho de pólvora retilíneo que termina no detonador”; “na haste e no rastilho e que este está contido no plano”).

Além disso, o vetor é paralelo ao vetor , então temos algo assim:

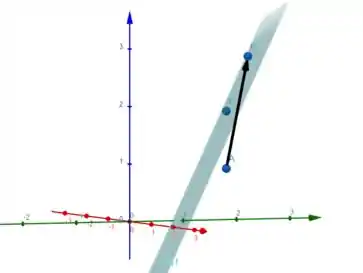
Nosso primeiro objetivo é encontrar o ponto , vamos ver como podemos fazer isso hahaha

Passo 2

Vamos criar uma reta que passa pelo ponto e pelo ponto . Seu vetor diretor vai ser , certo?

Então, essa reta vai ser

Boa, já encontramos uma reta:

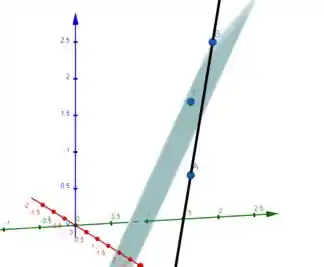
Passo 3

Agora precisamos encontrar o ponto para aí sim vermos quanto tempo leva pra tudo acontecer ok?

O ponto vai ser a intersecção da reta com o plano . Vamos encontrar!!

Um ponto genérico da reta , pela sua equação, é:

Vamos substituir esse ponto na equação do plano:

Então a intersecção entre a reta e o plano é dada quando , certo?

Vamos substituir esse no ponto genérico para encontrarmos o ponto :

Passo 4

Sabemos que:

Quando a pessoa acende a extremidade , o fogo percorre o caminho e depois o caminho , até o detonador. Então, como o fogo se propaga com velocidade unitária , vamos encontrar a distância entre os vetores e e assim encontraremos o tempo que o processo leva:

Se fizermos esse continha na calculadora, vemos que dá algo próximo de , que está entre 3 e 4, entãooo, ta provado!! :)

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam A = ( 2 ,1 ,1 ) , B = ( - 1 ,0 ,1 ) , C = ( 0 ,2 ,1 ) e π : X = 2 ,4 ,0 + α- 1 ,1 ,1 + β( - 2 ,- 1 ,0 ) . Prove que o lugar geométrico dos pontos X do plano π tais que o tetraedro tem volume 1 é

As retas r : X = 1 ,0 ,0 + α( 0 ,1 ,1 ) , s : X = 0 ,2 ,0 + β( 1 ,0 ,1 ) e t : X = 0 ,0 ,3 + γ( 1 ,1 ,0 ) são concorrentes com h , respectivamente, nos pontos A , B e C . Sabendo que B é o ponto médio

O plano π contém r : x - y = x + z - 1 = 0 e determina, com os planos coordenados, um tetraedro de volume 1 / 12 . Obtenha os vértices do tetraedro e uma equação geral de π .

Considere as retas r : X = 1 ,1 ,0 + λ( 0 ,1 ,1 ) e s :( x - 1 ) / 2 = y = z . Sejam A o ponto de interseção de s com o plano π , e B e C , respectivamente, os pontos que r intercepta O x z e O x y .

O paralelogramo A B C D tem os lados A B e C D paralelos a r : X = 0 ,0 ,0 + λ( 3 ,4 ,5 ) e os outros dois lados paralelos a π : x + y + 3 z = 0 . Sabendo que A = ( 0 ,0 ,0 ) e D = ( 1 ,1 ,1 ) , deter