Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 18.Exercício - Ex. 16

O paralelogramo A B C D tem os lados A B e C D paralelos a r : X = 0 ,   0 ,   0 + λ   ( 3 ,   4 ,   5 ) e os outros dois lados paralelos a π : x + y + 3 z = 0 . Sabendo que A = ( 0 ,   0 ,   0 ) e D = ( 1 ,   1 ,   1 ) , determine B e C .

Passo 1

Bom, note que a reta r contém o ponto A , isso é muito importante! Se A B é paralelo a r e r contém A , então sabemos que r também contém B . Assim, B é do tipo

B = 0 ,   0 ,   0 + k   3 ,   4 ,   5 = ( 3 k ,   4 k ,   5 k )

Temos, por enquanto, a seguinte situação:

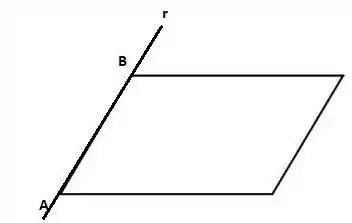
Não sabemos ainda qual vértice da figura é D ou C . Vamos chamar C = ( x ,   y ,   z ) . Assim,

D C → = x - 1 ,   y - 1 ,   z - 1 = λ   ( 3 ,   4 ,   5 )

Logo,

x - 1 = 3 λ y - 1 = 4 λ z - 1 = 5 λ

Da primeira equação, temos que

λ = x - 1 3

Substituindo nas demais:

y - 1 = 4 x - 4 3 z - 1 = 5 x - 5 3 ⇒ 3 y - 3 = 4 x - 4 3 z - 3 = 5 x - 5 ⇒ 4 x - 3 y = 1 5 x - 3 z = 2

Da primeira equação:

x = 1 + 3 y 4

Substituindo na segunda:

5 + 15 y 4 - 3 z = 2 ⇒ 5 + 15 y - 12 z = 8 ⇒ 15 y - 12 z = 3 ⇒ 5 y - 4 z = 1

Logo,

z = 5 y - 1 4

Portanto, o ponto C é do tipo

C = 1 + 3 y 4 ,   y ,   5 y - 1 4

Passo 2

Já temos que os pontos são da forma

B = 3 k ,   4 k ,   5 k           e           C = 1 + 3 y 4 ,   y ,   5 y - 1 4

Agora vamos olhar para o outro par de lados paralelos. Vamos supor que B D seja paralelo a A C . Esses dois lados devem ser paralelos ao plano π : x + y + 3 z = 0 , cujo vetor normal é

n → = ( 1 ,   1 ,   3 )

Assim, devemos ter

B D → ⋅ n → = 0               e           A C → ⋅ n → = 0

Portanto,

1 - 3 k ,   1 - 4 k ,   1 - 5 k ⋅ 1 ,   1 ,   3 = 0 ⇒ 1 - 3 k + 1 - 4 k + 3 - 15 k = 0

Logo,

22 k = 5 ⇒ k = 5 22

Portanto,

B = 15 22 , 20 22 , 25 22

Passo 3

Já para achar C , usamos A C → ⋅ n → = 0 . Assim,

1 + 3 y 4 ,   y ,   5 y - 1 4 ⋅ 1 ,   1 ,   3 = 0

Logo,

1 + 3 y 4 + y + 15 y - 3 4 = 0

Portanto,

1 + 3 y + 4 y + 15 y - 3 = 0 ⇒ 22 y = 2 ⇒ y = 1 11

Assim,

1 + 3 y 4 = 1 4 1 + 3 11 = 1 4 ⋅ 14 11 = 7 22

5 y - 1 4 = 1 4 5 11 - 1 = - 6 44 = - 3 22

Logo,

C = 7 22 , 1 11 ,   - 3 22

Resposta

B = 15 22 , 20 22 , 25 22

C = 7 22 , 1 11 ,   - 3 22

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma equação de plano para um plano que passe pelo ponto ( 1,5 , 1 ) perpendicular aos planos 2 x + y - 2 z = 2 e x + 3 z = 4 .
Determine se os planos são paralelos, perpendiculares, ou nenhum. Se não, ind ind o ângulo entre eles. (Arredondar uma casa decimal.) 9 x - 3 y + 6 z = 2 2 y = 6 x + 4 z
Onde a linha que passa por (- 3,1 , 0) e (- 1,5 , 6) intercepta o plano 2 x + y - z = - 2
Determine se os planos são paralelos, perpendiculares, ou nenhum. Se não, ind ind o ângulo entre eles. (Arredondar uma casa decimal.) 2 x - 3 y = z 4 x = 3 + 6 y + 2 z
Encontre uma equação de plano para um plano que passe pelos pontos ( 0 , - 2,5 ) e ( - 1,3 , 1 ) e seja perpendicular ao plano 2 z = 5 x + 4 y .