Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Hipérbole - Ex. 56
Encontrar uma equação da elipse com focos nos vértices da hipérbole e vértices nos focos dessa hipérbole.
Passo 1
Oi galera, tudo bem? Vamos resolver junto esse exercício? =D
Pra começar, você identifica que temos uma hipérbole de pé? O termo positivo é com o , isso indica a orientação dela! Outra coisa que dá pra ver logo de cara é que essa hipérbole está centrada na origem, pois não temos algo do tipo ou no numerador da equação dada. Sendo assim o centro é .
E, por falar na equação geral, vamos relembrar como é a equação geral da hipérbole de pé:
Comparando com a equação do enunciado:
Temos que e .
E da relação fundamental podemos encontrar o parâmetro :
Então a distância entre o centro e um dos focos da hipérbole é . Como essa hipérbole está de pé, os focos são e . Os vértices estão relacionados com o parâmetro , então os pontos dos vértices dessa hipérbole são e .
Beleza?
Passo 2
Agora vou desenhar a hipérbole e depois desenhar a elipse em cima pra gente ver a equivalência dos valores. Os vértices estão marcados pelas bolinhas vermelhas e os focos com as bolinhas roxas. Coloquei também os pontos da parte superior da hipérbole, os outros dois são simétricos e estão pra baixo do eixo . O esboço dessa hipérbole é:
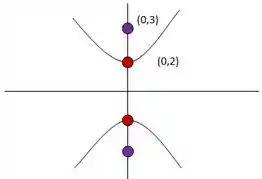
Tranquilo?
Agora por cima vou desenhar a elipse. Os focos dela vão ser os pontos vermelhos e consequentemente os vértices serão os pontos roxos. Ela também vai estar em pé, ou seja, o semi eixo maior é o vertical. O esboço (em verde) vai ficar assim:
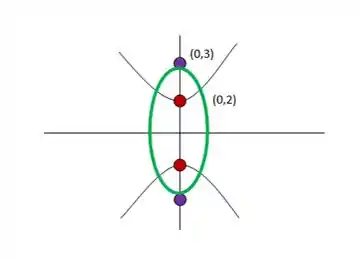
Agora temos que pensar na elipse e esquecer o que e da hipérbole significam e ficar apenas com os valores. Olhando para a elipse, a distância do centro até o ponto vermelho é o parâmetro , certo? E como essa distância vale , então na elipse. E a distância do centro até um dos vértices é o parâmetro , e no nosso desenho ele vale , então .
A relação fundamental da elipse é similar ao Pitágoras, então podemos achar o parâmetro , que é fundamental pra gente escrever a equação geral dela:
Beleza até aqui?
Passo 3
Agora vou te relembrar o que fizemos até aqui: temos o centro , os parâmetros e da elipse. Como ela é centrada na origem, não precisamos deslocar ela na equação. A equação geral é:
Substituindo e temos:
Multiplicando toda equação por temos:
Pronto! Conseguimos escrever a equação para essa elipse!
Espero ter ajudado!
Vamos pra próxima?