Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 26.Exercício - Ex. 6
No exercício anterior, reconheça cada curva e faça um esboço da superfície.
Passo 1
Para resolver esta questão, vamos ter que analisar cada curva diretriz obtida na questão 26-5 e depois fazer um esboço da superfície obtida no final da questão.
Então, vamos começar devagar, a partir da letra a). Lá, a diretriz dada foi:
Como a segunda superfície é um plano inclinado, não podemos isolar e substituir na equação de cima para observar a curva obtida.
Se fizermos isto, podemos distorcer o resultado real, visto que a curva obtida seria a projeção da curva real no plano . E então, como fazer?
Vamos analisar primeiro a nossa superfície . Ela é uma superfície cilíndrica parabólica, e suas diretrizes são paralelas ao eixo .
Automaticamente, ao interceptarmos a superfície por um plano, temos duas curvas possíveis: retas (uma ou duas), se o plano for paralelo ao eixo , ou uma parábola, caso contrário.
Então, vamos verificar se o plano é paralelo a . Para isto, temos o seguinte produto interno:
Como o produto interno deu diferente de zero, o plano não é paralelo a . Automaticamente, a curva é uma parábola!
Agora, vamos fazer o esboço da superfície . Para isto, iremos utilizar softwares para nos auxiliar.
Ao vocês fazerem o esboço, é importante sempre colocarem o vértice. Continuando, temos:
Passo 2
Agora, vamos para a letra b). Lá, a diretriz dada foi:
Como a segunda superfície é um plano paralelo a um dos planos coordenados, podemos isolar a sua variável e substituir na primeira equação.
Com isto, vamos obter:
Que é exatamente a primeira equação, já que ela não era função de . Continuando, a diretriz será:
Então, a diretriz é uma circunferência!
Agora, vamos fazer o esboço da superfície: . Para isto, iremos utilizar softwares para nos auxiliar.
Ao vocês fazerem o esboço, é importante sempre colocarem o vértice. Continuando, temos:
Passo 3
Agora, vamos para a letra c). Lá, a diretriz dada foi:
Como a segunda superfície é um plano paralelo a um dos planos coordenados, podemos isolar a sua variável e substituir na primeira equação.
Com isto, vamos obter:
Que é exatamente a primeira equação, já que ela não era função de . A equação da diretriz consiste na equação de uma hipérbole após uma rotação de 45° em torno de .
Então, a diretriz é uma hipérbole!
Agora, vamos fazer o esboço da superfície: . Para isto, iremos utilizar softwares para nos auxiliar.
Ao vocês fazerem o esboço, é importante sempre colocarem o vértice. Continuando, temos:
Passo 4
Agora, vamos para a letra c). Lá, a diretriz dada foi:
Como a segunda superfície é um plano paralelo a um dos planos coordenados, podemos isolar a sua variável e substituir na primeira equação.
Com isto, vamos obter:
Que é exatamente a mesma hipérbole obtida do passo anterior.
Para este caso, não iremos fazer um esboço do desenho, pois ele consiste apenas em pontos de um plano.
A ideia para o esboço desta cônica é o primeiro e quarto quadrante do plano (o que implica em ) mais a origem .
Resposta
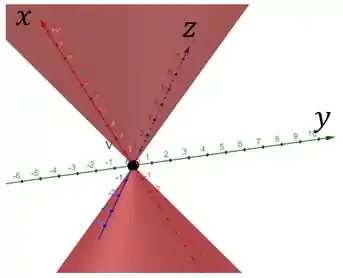
Para a letra a), a curva é uma parábola o esboço de é:
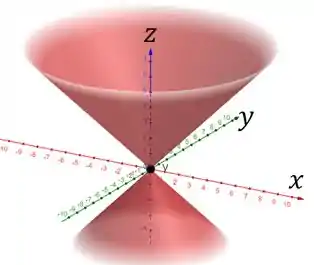
Para a letra b), a curva é uma circunferência o esboço de é:
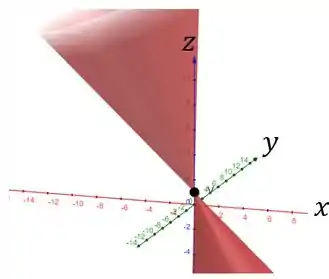
Para a letra c), a curva é uma hipérbole o esboço de é:
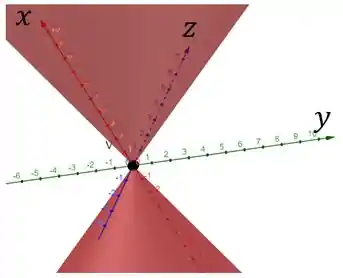
Para a letra d), a curva é uma hipérbole.